Transmission des images couleurs : Systèmes expérimentaux – Prise de vue – Procédé NTSC

Il existe actuellement trois systèmes de transmission d’une image en couleurs : le NTSC, le PAL et le SECAM. Nous allons voir dans ce chapitre le procédé NTSC, les autres procédés seront vus dans le chapitre suivant.

Nous allons examiner d’abord les contingences liées à la transmission d’une image en couleurs, puis nous passerons en revue, la plupart des solutions qui sont proposées pour résoudre tous ces problèmes. Après cela, nous pourrons examiner le système NTSC.

I – Production et transmission d’une image en couleurs

Vous savez déjà sans doute que pour imprimer une photographie en couleurs, on utilise les trois couleurs fondamentales qui sont appliquées successivement sur une même feuille de papier : l’effet global sur l’œil est la somme des trois effets partiels.

On peut procéder de même en télévision en couleurs, en mettant à profit la persistance rétinienne qui permet à l’œil de confondre ces impressions lumineuses à condition qu’elles se succèdent rapidement dans le temps.

On peut donc en fait, procéder de deux façons différentes :

Soit on présentera simultanément trois images colorées en couleurs primaires (rouge, vert et bleu), et on s’arrangera comme en imprimerie pour les superposer.

Soit on présentera les trois images colorées successivement, l’une après l’autre, aussi rapidement que possible, de façon que l’œil ne puisse distinguer les images partielles et les confonde en une seule impression colorée.

La première solution est mise à profit dans les systèmes SIMULTANES. La seconde solution est utilisée dans les procédés SEQUENTIELS.

A) Bande passante nécessaire à la transmission d’une émission en télévision couleurs

Les problèmes de bande passante ont été largement évoqués lors de l’examen de la télévision noir et blanc notamment dans le chapitre un. Reprenons succinctement l’explication afin de bien introduire les problèmes de bande passante posés en télévision couleurs.

Supposons que nous désirions transmettre une image en noir et blanc, avec une très grande définition, c'est-à-dire que nous voulions respecter au maximum tous les fins détails, toutes les nuances des gris, tout l’aspect fouillé de l’image. Nous considérons d’autre part, qu’une image en 625 lignes (définition verticale) donne un résultat satisfaisant.

L’image de télévision étant au format 4/3, la définition horizontale doit être :

830 lignes ou points

Cette notion de définitions horizontale et verticale peut être traduite par le nombre de points à transmettre.

Ainsi dans notre cas, nous devons transmettre :

625 x 830 = 520 000 points par image

Or, on transmet 25 images par seconde (en 50 demi images ou trames), le nombre total des points transmis par seconde est donc :

520 000 x 25 = 13 000 000 points / s

L’image la plus fine que l’on puisse obtenir avec deux points est constituée d’un point blanc suivi d’un point noir. Or, le point blanc correspond à l’alternance positive du signal vidéo et le point noir à l’alternance négative de ce même signal vidéo. La période du signal est donc composée de deux points.

La fréquence maximale du signal vidéo donc la bande passante nécessaire pour transmettre cette information sera égale à :

= 6 500 000 Hz = 6,5 MHz

Si l’on veut maintenant conserver la même finesse dans les détails de l’image colorée que sur l’image en noir et blanc, il faudra transmettre trois fois plus de points. En effet, il faudra transmettre en une seconde 13 000 000 de points dans l’image bleue, 13 000 000 de points dans l’image verte et 13 000 000 de points dans l’image rouge, soit 39 000 000 de points.

La bande passante nécessaire est donc maintenant triplée :

Bp    = 6,5 x 3 = 19,5 MHz.

On peut bien sur tourner la difficulté, si l’on désire transmettre les 39 000 000 de points dans une bande passante de 6,5 MHz seulement.

Il suffit tout simplement de tripler la durée de la transmission.

Il y a en effet une loi physique que l’on peut transgresser : c’est la loi de la conservation du produit :

BANDE PASSANTE x TEMPS

La (figure 1) représente ce produit : c’est la surface du rectangle hachuré. La surface représente la quantité d’informations que l’on désire transmettre. On peut transmettre cette quantité d’informations en un temps très bref, mais il faut alors que la bande passante soit très grande.

On peut aussi se permettre une transmission lente (donc pendant un temps relativement long) et alors la bande passante peut être réduite.

Mais quoique l’on fasse, on ne peut échapper à cette loi, il va donc falloir composer.

B) Procédés simultanés

On se propose donc de transmettre simultanément les trois images en couleurs fondamentales. Le système le plus simple qui se présente immédiatement à l’esprit est de tripler la chaîne de transmission.

A l’émission, on prend trois caméras, chacune d’elles est munie d’un filtre coloré : rouge, vert et bleu. Chaque caméra analyse donc une image primaire. L’information électrique correspondant à cette image est envoyée sur un émetteur et le signal modulé est véhiculé par une fréquence porteuse particulière (figure 2) .

A la réception, trois antennes captent les trois signaux : chaque antenne alimente un récepteur de télévision complet. Les cathoscopes   des récepteurs sont bien sur de phosphorescence différente : l’un est composé de phosphore rouge, l’autre de phosphore bleu et le troisième de phosphore vert. Les trois images ainsi obtenues sont superposées, grâce à l’emploi de miroirs dichroïques (figure 3) .

Un miroir dichroïque est obtenu par dépôt d’une couche métallique très fine sur du verre et qu’il présente alors la propriété de laisser passer une des couleurs fondamentales et d’en réfléchir une autre.

Inconvénients d’un tel procédé :

Il faut disposer de trois fréquences différentes. Or, l’encombrement spectral est déjà tel, que l’on arriverait vite à la saturation.

La bande passante globale est trois fois plus grande qu’en noir et blanc.

La superposition des trois images est toujours délicate (parallaxe d’espace). Si elle n’est pas réalisée parfaitement, les couleurs bavent.

Améliorations apportées

Les cathoscopes utilisés sont des cathoscopes ordinaires, et on interpose devant eux, des filtres colorés.

Certaines parties des émetteurs peuvent être communes. Cependant, on n’échappe pas à la nécessité d’une bande passante triple.

Ce procédé simple en apparence, était voué à l’échec. Il a été rapidement abandonné.

C) Procédés séquentiels

Un procédé simple consiste, à l’émission, à analyser l’image en faisant tourner un disque à secteurs colorés devant la caméra. Le disque comporte trois filtres, un rouge, un vert et un bleu qui tournent rapidement devant le tube analyseur (figure 4) .

A la réception, un disque identique, tournant en parfaite synchronisation avec celui de l’émission, restitue par persistance rétinienne, une image colorée.

L’avantage le plus important d’un tel système est que l’on peut utiliser une chaîne de transmission normale.

Malheureusement, à raison de 25 images par seconde (standard normal), on n’obtient que 25/3 = 8,333 images de chaque couleur par seconde.

Un effet très désagréable de papillotement de couleurs se fait alors sentir car la persistance rétinienne est insuffisante.

Pour remédier à ce défaut, on double la vitesse de rotation du disque et le nombre de secteurs colorés.

Ainsi, en mettant à profit le balayage entrelacé, on transmet à chaque trame une demi image colorée, et on en profite pour changer de couleur à chaque demi image.

Malheureusement, le résultat, bien que meilleur, n’est pas encore tout à fait satisfaisant et il subsiste un papillotement gênant. Voyons maintenant un système plus performant.

1) Premier système C.B.S.

En 1940, la C.B.S.(Columbia Broadcasting System) expérimente le procédé suivant :

Chaque trame est explorée en 1/120^ème seconde et deux trames consécutives sont entrelacées et comportent 343 lignes.

L’ordre de succession est le suivant :

Trame impaire bleue

343 lignes

Trame paire verte

Image Trame impaire rouge

343 lignes

Colorée Trame paire bleue

Trame impaire verte

343 lignes

Trame paire rouge

Ainsi, une image est retransmise par une trame d’une certaine couleur et une autre trame d’une autre couleur. Le papillotement est ainsi un peu réduit.

Mais l’inconvénient majeur de ce système est qu’il ne permet pas de recevoir en noir et blanc sur un récepteur noir et blanc les émissions faites en couleurs. On dit que le système n’est pas compatible. De plus, l’image ne comporte que 343 lignes (le standard américain comporte 525 lignes pour les émissions en noir et blanc). Pour remédier à ce défaut, la C.B.S. a modifié son système.

2) Second système C.B.S.

En 1945, la C.B.S. présente un système semblable mais s’adaptant au standard 525 lignes. Les six filtres sont disposés sur un tambour (quelquefois sur un disque). Chaque filtre est substitué au précédent toutes les 1/144^e de seconde, ce qui correspond à 24 images complètes par seconde (figure 5) .

Inconvénients, le système n’est pas compatible, le balayage vertical correspond à 24 images par seconde, au lieu de 30 images en noir et blanc. De plus, le scintillement reste encore notable, des franges colorées apparaissent lorsque l’objet télévisé se déplace rapidement (c’est ce que l’on appelle la parallaxe de temps), à chaque mouvement de l’œil ou de la tête de l’observateur, il apparaît des éclairs colorés.

Malgré tous ces inconvénients, la C.B.S. a réussi à faire normaliser ce système aux Etats-Unis en 1951. En juin 1951, les émissions publiques commencèrent : ce fut un échec total : deux cents téléviseurs furent vendus en quatre mois, alors qu’il existait à l’époque plus de six millions de téléviseurs en noir et blanc. Ce procédé fut alors définitivement abandonné.

D) Procédés optiques

Nous avons vu jusqu’à maintenant comment nous pouvions reconstituer une image en couleurs, en partageant entre les trois couleurs, la bande passante (procédé simultané) ou le temps (procédé séquentiel). On peut imaginer un système qui partage la surface du tube analyseur à l’émission et du cathoscope à la réception.

1) Procédé C.T.I.

Imaginé aux Etats-Unis par la C.T.I. (Color Télévision INC) et étudié à fond par les laboratoires Razeltine, ce procédé conduisait à juxtaposer les trois images primaires sur la surface du tube analyseur (figure 6) .

Les trois images sont alors balayées en une seule fois. A la réception, un système de miroirs munis de filtres superpose les trois images en redonnant les couleurs d’origine.

En examinant la (figure 6 b) , on remarque la très mauvaise utilisation de la surface du tube analyseur. On a essayé alors d’anamorphoser l’image pour occuper une surface plus grande.

2) procédé Y. Angel

Pour recouvrir le maximum de la surface du tube analyseur, Y. Angel utilise un objectif anamorphoseur, qui a pour but de comprimer l’image en largeur. On peut ainsi loger trois images côte à côte, comme dans le procédé C.T.I., mais avec l’avantage d’exploiter mieux l’écran de la caméra d’analyse (figure 7) .

Les trois images sont ici encore balayées en une seule fois. Mais un handicap très grand apparaît : il faut que les trois objectifs anamorphoseurs soient parfaitement identiques.

Le moindre décalage dans la superposition des images, le moindre défaut anamorphosique, provoquent un mauvais registre des images et des franges colorées apparaissent.

3) Procédé quadrichrome

On peut alors penser supprimer l’inconvénient des objectifs anamorphoseurs et imaginer un système utilisant la quadrichromie (au lieu de la trichromie). Nous savons que le rendu des couleurs ne peut être qu’amélioré.

Au lieu de juxtaposer trois images, nous allons placer quatre images côte à côte : une image rouge, une image verte, une bleue et une jaune (figure 8) .

Avantages de ce procédé

La surface du tube analyseur est mieux utilisée.

Il n’y a pas l’inconvénient des objectifs anamorphoseurs de prix élevé.

Le balayage des quatre images s’effectue toujours en une seule fois.

Le rendu des couleurs est bien meilleur.

On peut recevoir l’image en noir et blanc sur un récepteur noir et blanc en modifiant légèrement quelques réglages de celui-ci.

1) On peut par exemple, dilater l’image dans le sens vertical et dans le sens horizontal, de manière à couvrir la totalité de l’écran du récepteur avec une seule image fondamentale.

2) On peut doubler la fréquence de balayage horizontal et vertical de façon à superposer les quatre images. L’image en noir et blanc obtenue serait parfaite si les quatre images registraient parfaitement : c’est là la plus grande difficulté.

3) Si on ne veut pas toucher aux réglages du récepteur noir et blanc, on peut tout simplement superposer les quatre images à l’aide d’un jeu de miroirs avec, bien sur, la même difficulté de superposition que ci-dessus.

4) On peut aussi mettre un cache qui masquerait trois images : l’image finale serait alors de dimensions quatre fois plus réduites.

On commence à entrevoir les problèmes qui se posent pour insérer un système de télévision en couleurs dans un parc de téléviseurs noir et blanc.

En effet, il faut pour qu’un système de télévision en couleurs soit viable  que :

Une émission en couleurs soient reçue par les téléviseurs noir et blanc existants, c’est la compatibilité directe.

Une émission en noir et blanc soit reçue en noir et blanc par les téléviseurs couleurs, c’est la compatibilité inverse.

Il faut en outre que les téléviseurs couleurs soient universels, c'est-à-dire qu’ils captent les émissions en couleurs et les émissions en noir et blanc sans aucune manipulation des réglages.

Jusqu’à présent, tous les systèmes que nous avons vus, n’étaient pas compatibles. Nous reviendrons sur ce sujet très important à maintes reprises.

5) Procédé E.M.I.

Nous avons vu précédemment qu’il était possible d’obtenir une bonne solution, soit par le système à trois voies, soit par le système successif.

Sous sa forme initiale, seul le système à trois voies (procédé simultané) permettait d’obtenir à tout instant, les trois composantes colorées de l’image. Nous avons souligné alors l’existence de franges colorées que nous avons indiqué comme dues à des erreurs de parallaxe. Il est en effet pratiquement impossible d’obtenir trois tubes, trois optiques et trois analyses rigoureusement identiques.

C’est pour cette raison qu’en 1954, la société Anglaise E.M.I. (Electric and Musical Industries), suivie par la Général Electrico Co, aux Etats-Unis, a essayé de combiner les deux procédés en un seul (figure 9) .

A l’émission, l’équipement est allégé considérablement par utilisation d’une seule caméra de prise de vue ne comportant qu’un seul tube analyseur muni du fameux disque à secteurs colorés.

La succession des filtres se fait à raison de 150 par seconde (3 x 50), la définition verticale est celle du standard britannique de 405 lignes, ce qui conduit à une bande passante de 7,5 MHz pour le spectre vidéo.

Ces signaux sont alors amplifiés, puis appliqués sur trois tubes cathodiques à forte persistance, mais pendant 1/150^ème de seconde seulement. Ainsi, l’image rouge est appliquée au cathoscope rouge, la verte au cathoscope vert et la bleue au cathoscope bleu.

La voie de chacun des tubes n’est ouverte que pendant un temps très bref (1/150^ème de seconde) et cette commande s’effectue à l’aide d’un commutateur électronique. Grâce à la persistance du cathoscope, les images R, G et B persistent au moins pendant 1/50^ème de seconde et peuvent donc être analysées normalement par les trois tubes analyseurs.

Le système que l’on obtient donc finalement est un procédé simultané qui peut être dans les normes standard CCIR de 625 lignes et 50 analyses verticales par seconde. De plus, le spectre peut être réduit à 4,6 MHz.

Ce procédé permet aussi par la suite, de réduire les bandes des canaux rouge et bleu par exemple en laissant intacte la bande du canal vert.

Autre avantage possible, les franges colorées dues à la parallaxe de temps disparaissent. Ce système a été appelé CHROMA CODER.

E) Procédés améliorés

Les procédés séquentiels seraient compatibles si l’on pouvait conserver la même fréquence pour le balayage vertical. Mais le phénomène gênant du papillotement des couleurs ne permet pas cette solution. D’autre part, l’augmentation de la fréquence image entraîne une augmentation de la bande passante nécessaire, que l’on peut d’ailleurs compenser par une diminution du nombre de lignes. Mais dans les deux cas, ce système est alors incompatible.

Les procédés simultanés ne sont pas compatibles car chacun des trois émetteurs ne conservent pas les normes du standard noir et blanc. De plus, le procédé simultané à trois émetteurs n’est pas viable à cause du spectre triple qu’il occuperait.

Les procédés optiques seraient compatibles mais à condition d’accepter certaines déformations de l’image. De plus, les récepteurs monochromes devraient subir une légère modification pour recevoir les images couleurs.

Tous les procédés vus jusqu’à présent utilisaient soit un spectre anormalement large, soit des normes différentes de balayage. Le dernier système que nous avons vu se rapprochait des normes usuelles, puisqu’il utilisait une largeur de spectre égale à celle du noir et blanc et que le balayage et la définition étaient classiques.

1) Les Mixed Highs (Hautes fréquences mélangées)

Jusqu’en 1946, il paraissait normal que l’encombrement du spectre pour une image en couleurs soit trois fois plus grande que pour une image en noir et blanc. C’est la découverte vers cette époque d’une propriété de l’œil, qui permet d’envisager une réduction du spectre.

On remarqua qu’il était impossible de discerner la couleur individuelle des petits détails d’une image en couleurs. Les détails étaient bien sur visibles, mais seules les grandes plages avaient des couleurs discernables.

C’est ce que nous avons vu dans le chapitre 14 et que nous avons exprimé en disant que l’acuité visuelle de l’œil était plus faible pour la couleur que pour le noir et blanc.

On savait aussi, d’autre part, depuis 1936, qu’il était possible de filtrer un spectre de télévision, de le couper en deux, trois ou plusieurs tranches, de transmettre ces morceaux sur des voies séparées, puis, à l’arrivée, de recomposer ces morceaux pour obtenir enfin une image normale.

C’est un peu le jeu de puzzle. On décompose l’image en petits morceaux et on le reconstitue à l’arrivée. Le système des MIXED HIGHS découle directement de ces notions (figure 10) .

A l’émission, chacune des voies rouge, verte et bleue utilise un spectre vidéo de 4 MHz. A l’aide de filtres, on décompose chaque signal en deux signaux :

L’un dont le spectre s’étend de 0 à 2 MHz (et baptisé pour la circonstance les basses fréquences ou BF).

L’autre dont le spectre s’étend de 2 à 4 MHz est baptisé les hautes fréquences ou HF.

Les hautes fréquences de voies rouge (HF R) et bleue (HF B) sont mélangées au signal vert.

Ce mélange s’effectue très simplement dans une matrice composée de résistances (figure 11), les résistances R découplent les différentes voies entre elles, le signal des MIXED HIGHS étant récupéré aux bornes de la résistance R’.

Le signal composé des hautes fréquences mélangées, module un émetteur, tandis que les basses fréquences rouge (BF R) et bleue (BF B) modulent deux émetteurs distincts (un peu comme dans le système simultané à trois voies).

Mais cette fois, le spectre total occupé n’est plus de 18 MHz (figure 12 a) mais de l’ordre de 12 MHz seulement (figure 12 b) .

6 MHz (image verte + HF mélangée) + 2 MHz (BF rouge) + 2 MHz (BF bleue) + Son = 12 MHz

Procédé à la réception

On croyait à l’époque qu’il était absolument nécessaire de reconstituer les images rouge et bleue avec leur spectre normal. On extrayait pour cela de l’image verte les hautes fréquences communes, et on les mélangeait aux basses fréquences R et B pour reconstituer les deux images.

On retrouvait ainsi trois images complètes (figure 13) .

L’image verte peut être utilisée directement pour les récepteurs en noir et blanc (la première condition de la compatibilité peut être considérée comme remplie).

La deuxième condition de la compatibilité est remplie aussi, puisque le récepteur couleur peut recevoir une émission en noir et blanc sur sa voie MIXED HIGHS.

Le seul inconvénient est le débordement du spectre.

Hazeltine s’est alors attaqué au problème et s’est aperçu en 1951, que l’on pouvait fort bien filtrer les voies à l’émission non plus à partir de 2 MHz, mais de 1 MHz seulement.

Ainsi, les basses fréquences s’étendaient de 0 à 1 MHz.

Les hautes fréquences couvraient de 1 à 4 Mhz et étaient mélangées comme à l’habitude au signal vert.

Cette amélioration permettait donc de réduire le spectre à 8,5 MHz au lieu de 12 MHz (figure 14 c) .

6 MHz (image verte + HF mélangées) + 1 MHz (BF R) + 1 MHz (BF B) + Son = 8,5 MHz

A la réception, on s’est aperçu, d’autre part, qu’il était inutile d’extraire les hautes fréquences rouge et bleue pour reconstituer les trois images. Il suffisait d’avoir une image verte (BF G + HF G + HF R + HF B) à haute définition (puisque toutes les fréquences élevées de ce signal n’allaient que de 0 à 1 MHz) et enfin une image bleue à basse définition (BF B) pour la même raison que ci-dessus.

L’image totale en couleurs reproduite était cependant excellente, aussi bonne que dans le premier cas.

Le système restait toujours compatible et l’image reproduite sur un récepteur noir et blanc était toujours aussi bonne, puisque l’on n’avait pas touché à la définition de l’image verte.

Ne voulant pas s’arrêter en si bon chemin, Hazeltine a essayé de réduire encore la bande passante des images rouge et bleue. Il filtrait les signaux R et B à partir de 0,1 MHz seulement.

Cela signifie que la bande passante des signaux R et B s’étendait seulement de 0 à 100 kHz (les hautes fréquences mélangées s’étendaient par contre de 0,1 MHz à 4 MHz).

Et l’image couleur restait bonne.

On avait donc économisé la bande passante globale puisqu’elle occupait un spectre de 6,5 MHz (figure 14 d) , c'est-à-dire un spectre très proche du standard noir et blanc normal (6 MHz).

6 MHz (MIXED HIGHS) + 0,1 MHz (BF R) + 0,1 MHz (BF B) + Son = 6,5 MHz

Dans ce système, le codage était donc combiné avec la transmission. C’est donc vraiment le premier pas vers la compatibilité complète.

La grande leçon que l’on en a retiré, est donc que l’on peut réduire le spectre des images rouge et bleue dans des proportions considérables, et que l’image colorée résultante reste bonne, à condition que l’image verte conserve sa définition totale avec en plus, les fréquences élevées des images R et B.

2) Procédé des points intercalés

A l’émission, les caméras R, G et B délivrent les signaux électriques R, G et B avec un spectre égal à celui du noir et blanc, soit de 4,5 MHz pour le standard américain (figure 15) .

Les canaux R, G et B sont filtrés comme dans le cas des MIXED HIGHS, c'est-à-dire, à l’aide de filtres passe bas (0 – 2 MHz), et de filtres passe haut (2 – 4,5 MHz).

On obtient ainsi les hautes fréquences des signaux R, G et B (que nous appellerons HF R, HF G et HF B) qui sont mélangées dans une simple matrice à résistances (figure 11) .

Ces hautes fréquences sont mélangées en permanence dans le temps.

Les basses fréquences des signaux R, G et B (que nous appellerons BF R, BF G et BF B) sont, par contre, envoyées dans un circuit d’échantillonnage qui a pour but de transmettre successivement, un échantillon du rouge, un échantillon du bleu et un échantillon du vert et ainsi de suite….

La durée de transmission de ces échantillons successifs doit être suffisamment brève pour que le point d’analyse correspondant soit peu apparent sur l’image.

Un échantillon de couleur est transmis toutes les 0,0877 s : sa durée est donc très brève.

Les trois échantillons (R, G et B) sont donc transmis en :

0,0877 x 3 = 0,2631 s

La fréquence d’échantillonnage est par conséquent de :

f échantillonnage = 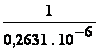= = 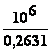3,8 MHz

Les impulsions rouges, vertes et bleues, sortent donc mélangées du circuit d’échantillonnage (figure 16) .

Ces impulsions sont envoyées dans un filtre passe bas dont la fréquence de coupure est égale à 4 MHz. Les impulsions sont donc transformées en sinusoïdes à fréquence de 3,8 MHz.

La fréquence des sinusoïdes est égale précisément à la fréquence de succession des impulsions. En effet, les impulsions correspondant à une même couleur se succèdent dans le temps, à 0,2631 s, c'est-à-dire que leur fréquence de répétition est de 3,8 MHz.

Les sinusoïdes R, G et B ainsi obtenues, comportent une composante continue. Vous remarquerez qu’elles ont aussi la propriété de passer par un maximum, au moment précis de l’échantillonnage de la couleur correspondante et de s’annuler au moment précis où les deux autres impulsions passent par leur maximum.

Ces trois sinusoïdes mélangées à la sortie du filtre passe bas constituent une sinusoïde unique, de fréquence 3,8 MHz et comportant elle aussi une composante continue.

Ainsi, la sinusoïde résultante a précisément la valeur des impulsions de couleur aux temps de l’échantillonnage. Cette simple sinusoïde superposée à une composante continue, contient donc toutes les informations nécessaires à la restitution de l’image initiale en couleurs.

Le signal des hautes fréquences mélangées et le signal des basses fréquences mélangées en succession, sont ensuite mélangés ensemble et modulent une fréquence porteuse unique.

A la réception, le signal reçu est donc composé des hautes fréquences mélangées et des basses fréquences mélangées en succession.

Au sortir de la détection vidéo, ce signal passe dans un filtre double passe haut et passe bas (figure 17) . Le filtre passe haut permet de récupérer les signaux HF mélangés.

Le filtre passe bas permet, lui, de récupérer les signaux BF mélangés qui sont alors envoyés dans un dispositif d’échantillonnage, fonctionnant en synchronisme parfait avec celui de l’émission (figure 18) .

Le circuit d’échantillonnage délivre donc des impulsions R, B et G se succédant dans le temps dans le même ordre qu’à l’émission. Chacune de ces impulsions est alors dirigée vers un filtre passe bas à fréquence de coupure de 4 MHz d’où elle ressort sous forme d’une sinusoïde à 3,8 MHz.

Les trois sinusoïdes correspondant au rouge, vert et bleu, peuvent alors être mélangées respectivement aux hautes fréquences. Les trois informations de couleur ayant ainsi été retrouvées, sont appliquées aux cathoscopes récepteurs (ou au cathoscope unique) et reconstituent ainsi l’image initiale en couleurs.

Amélioration du système

L’image reconstituée sur l’écran du cathoscope, se présente sous la forme d’une trame fine composée de points intercalés (d’où le nom du système) .

On peut améliorer encore la qualité de la reproduction, si l’on prend soin de renouveler la couleur des points élémentaires, à chaque analyse verticale. Pour atteindre ce but, il suffit tout simplement de lier la fréquence de succession des points (c'est-à-dire f = 3,8 MHz) à la fréquence d’analyse horizontale (f) par un rapport tel qu’une demi période soit gagnée au bout d’une ligne.

Si f est la fréquence des points et f la fréquence de balayage horizontale, il faut que l’on ait :

f = ( 2 k + 1 ) (k nombre entier quelconque)

C'est-à-dire que la fréquence d’échantillonnage du point soit égale à un multiple impair de la demi fréquence lignes.

Le système des points intercalés est compatible. Ainsi, le signal complexe (HF mélangées + BF mélangées) appliqué à un récepteur noir et blanc classique donnera une image compatible.

Cependant, du fait que les BF mélangées se présentent sous forme d’impulsions, elles vont se comporter comme si une fréquence parasite (à 3,8 MHz) était introduite dans le signal vidéo normal. Ce signal parasite va donner un pointillé de l’image.

Si la fréquence des points est quelconque par rapport à la fréquence de balayage lignes, ce pointillé va se présenter comme sur la (figure 19 a) (ces points seront relativement visibles).

Si l’on s’arrange maintenant pour que la fréquence des points soit liée à la fréquence de balayage lignes par un rapport tel que celui indiqué ci-dessus, les points vont s’intercaler et leur visibilité sera nettement diminuée (figure 19 b) .

Pour bien comprendre le mécanisme de ce phénomène, nous supposerons, pour simplifier, que le balayage vertical de notre téléviseur (noir et blanc par exemple) n’est pas entrelacé (ce qui n’enlève rien au rigoureux de la démonstration).

Supposons encore (toujours dans le but de simplifier les dessins) que la fréquence d’échantillonnage des points f est basse, mais qu’elle est liée à la fréquence de lignes par le rapport indiqué plus haut.

Dans le standard CCIR à 625 lignes, la fréquence de balayage horizontal est :

f = 625 x 25 = 15 625 Hz

La demi fréquence lignes est donc :

= = 7,8125 kHz

Supposons alors que la fréquence d’échantillonnage des points soit égale à cinq fois (nombre impair) f / 2, soit :

f = 5 x 7,8125 = 39,0625 kHz

La forme d’onde f est sinusoïdale : elle donnera donc sur l’écran du téléviseur (noir et blanc ou couleur), cinq oscillations (cinq alternances positives et cinq alternances négatives) complètes dans un temps correspondant au balayage de deux lignes successives (puisque f = 15 625 Hz).

Pendant la ligne numéro un, nous aurons donc (figure 20) , trois alternances positives et deux négatives. Pendant la ligne numéro deux, nous aurons, au contraire, trois alternances négatives et deux positives.

Pendant la troisième ligne et par conséquent pendant toutes les lignes impaires, le cas de la première ligne va se renouveler. De même, pendant la quatrième ligne et pour toutes les lignes paires, le cas de la ligne numéro deux va se répéter.

Supposons que les alternances positives du signal donnent des points blancs et que les alternances négatives donnent des points noirs.

Pendant la première ligne et pour toutes les lignes impaires et en particulier, la ligne numéro 625, nous aurons donc trois plages blanches, alternant avec deux noires. Pendant la deuxième ligne (et pour toutes les lignes paires), nous aurons au contraire, trois plages noires et deux blanches.

Pour l’image suivante, le phénomène s’inverse : en effet, les lignes d’une image étant au nombre de 625, la dernière ligne de l’image un est une ligne impaire. La ligne suivante, qui correspond à la ligne numéro un de l’image deux est donc une ligne paire.

Les images un et deux se superposent dans le temps et grâce à la persistance rétinienne, ces deux images sont vues simultanément : les effets se superposent aussi et l’image est vue uniformément grise.

Nous avons supposé jusqu’à maintenant, que le signal f était de fréquence relativement basse (39,0625 kHz).

En réalité, la fréquence f est beaucoup plus élevée (3,8 MHz), c'est-à-dire prés de cent fois plus grande. Au lieu d’avoir des plages blanches et noires, nous aurons des points alternativement blancs et noirs.

En pratique, les effets résultants sont un peu moins bons, car les deux images successives ne s’effacent pas complètement. Les points sont très fortement atténués mais restent encore visibles, si l’on observe l’écran à faible distance.

A distance normale d’observation de l’écran (c'est-à-dire quatre à cinq fois la diagonale de l’écran, soit 2,5 à 3 m pour un cathoscope de 59 cm), les points sont pratiquement invisibles.

Nous venons de voir qu’un signal parasite (f = 3,8 MHz) introduit à l’intérieur d’un spectre vidéo normal (0 à 4,5 MHz) se traduisait par un pointillé de l’image. Plus la fréquence parasite est élevée, moins ce pointillé est visible.

F) Spectre des raies

1) Modulation en amplitude d’une onde HF par un signal sinusoïdal BF

Soit une fréquence porteuse (f) , modulons cette fréquence HF par un signal sinusoïdal BF (F) (figure 21) . Vous savez que nous allons obtenir dans le spectre des fréquences, trois raies parfaitement définies : une raie à la fréquence HF (f), une raie HF égale à la somme (f + F) et une autre raie HF égale à la différence (f – F).

La quatrième raie est, bien sur, la raie à fréquence basse (F) que l’on néglige souvent, étant donné sa position très éloignée dans le spectre.

Exemple : soit une fréquence HF à moduler. Elle aura pour valeur : f = 1 MHz (1 000 000 Hz).

Modulons cette porteuse par un signal sinusoïdal BF dont la fréquence sera F = 1 000 Hz.

Les quatre raies que nous allons obtenir dans le spectre des fréquences seront :

a) F = 1 000 Hz (BF modulante)

b) f = 1 000 000 Hz (fréquence de la porteuse)

c) f + F = 1 000 000 + 1 000 = 1 001 000 Hz

d) f – F = 1 000 000 – 1 000 = 999 000 Hz

On comprend maintenant la raison pour laquelle on néglige souvent de représenter les fréquences BF : elles se trouvent très bas dans le spectre et ne sont pas gênantes.

Nous retiendrons qu’une onde HF modulée par un signal sinusoïdal, est traduite dans le spectre par trois fréquences HF : (f), (f + F), (f – F).

2) Modulation en amplitude d’une onde HF par un signal non sinusoïdal périodique

Un signal non sinusoïdal périodique, peut être décomposé en une somme de signaux sinusoïdaux de fréquences F, 2F, 3F, …. nF, F étant la fréquence de répétition du signal périodique, et n étant un nombre entier quelconque (c’est ce qu’on appelle la décomposition en série de Fourier).

Prenons un exemple, soit un signal BF périodique de période T = 1 ms et non sinusoïdal tel celui représenté (figure 22 a) .

La fréquence fondamentale de ce signal, c'est-à-dire sa fréquence de répétition est :

F = = = 1000 Hz

Il peut être décomposé en une somme de signaux sinusoïdaux dont les fréquences sont :

F = 1 000 Hz, 2 F = 2 000 Hz, 3 F = 3 000 Hz, etc.….

Supposons maintenant que ce signal module une onde porteuse. Si la fréquence de l’onde porteuse est 1 MHz, le spectre total sera composé des raies suivantes :

a) Partie basse fréquence : 1 000 Hz, 2 000 Hz, 3 000 Hz …….

b) Partie haute fréquence : 1 MHz (fréquence de l’onde porteuse)

1 001 000 Hz, 1 002 000 Hz, 1 003 000 Hz etc. ….

Et aussi

999 000 Hz, 998 000 Hz, 997 000 Hz etc. …..

La (figure 22 b) montre les différentes raies groupées autour de la fréquence de l’onde porteuse. Toutes les raies sont donc distantes les unes des autres de la valeur de la fréquence fondamentale.

3) Spectre vidéo

Le spectre vidéo est interrompu périodiquement à chaque ligne (c'est-à-dire 15 625 fois par seconde) pour un standard 625 lignes, en effet, la fréquence de balayage lignes est 15 625 Hz et l’image transmise est interrompue à chaque fin de ligne, pour permettre la transmission des impulsions de synchronisation.

De plus, l’image est encore interrompue toutes les 1/25^ème de seconde correspondant à la transmission des impulsions de synchronisation images. Si l’on considère de plus, que l’image globale transmise en 1/25^ème de seconde est en fait composée de deux demi images entrelacées, transmises chacune en 1/50^ème de seconde, on comprendra qu’il y a interruption périodique par les impulsions lignes et par les impulsions images. La (figure 23 a) représente un signal vidéo d’une image télévisée.

Il n’y a que quelques lignes représentées sur ce dessin, mais il est bien évident qu’il y a 625 : 2 = 312,5 lignes complètes dans l’intervalle d’une demi image.

La (figure 23 b) représente un signal vidéo d’une image noire. Il n’y a donc que les impulsions de synchronisation lignes et images qui y figurent.

On peut découper ce signal périodique non sinusoïdal en une somme de signaux sinusoïdaux.

1) L’interruption périodique correspondant aux impulsions lignes donne un spectre composé d’un nombre très élevé d’harmoniques de la fréquence de balayage lignes. Ce spectre sera celui indiqué sur la (figure 24) : chaque raie est distante de la précédente de 15 625 Hz bien entendu. Il existe une raie pour la fréquence zéro (c’est celle qui correspond à la composante continue du signal).

La fréquence f1 représente la fréquence fondamentale ou première harmonique.

La fréquence f2 représente la deuxième harmonique (31 250 Hz).

La fréquence f3 représente la troisième harmonique (46 875 Hz).

La fréquence f320 représente la 320^ème harmonique (5 MHz) etc. …

2) L’interruption périodique correspondant aux impulsions images donne un spectre composé d’un nombre très élevé d’harmoniques de la fréquence de balayage images (soit 50 Hz). Ce spectre sera donc celui indiqué sur la (figure 25 a) : chaque raie est distante de la précédente de 50 Hz.

Tout se passe donc comme si un signal non sinusoïdal à fréquence 50 Hz modulait un signal non sinusoïdal à 15 625 Hz.

Chaque raie à 15 625 Hz se trouve donc accompagnée de part et d’autre d’un certain nombre de raies distantes entre elles de 50 Hz (figure 25 b) et (figure 26) .

Ces raies sont parfaitement déterminées et immobiles dans le spectre.

Que se passe t’il maintenant lorsque l’image transmise n’est plus noire mais quelconque ?

En modifiant le contenu de l’image transmise, on modifie l’amplitude des différentes raies ainsi que leur nombre, mais pas leur position, puisque les fréquences de balayage lignes et images sont définies une fois pour toutes.

Par contre, le nombre de raies dépend de la fréquence maximum contenue dans le signal vidéo. Ainsi, par exemple, pour un standard européen où le spectre vidéo s’étend de 0 à 5 MHz, la fréquence maximum transmise est de 5 MHz et le nombre de raies harmoniques de la fréquence lignes sera :

Nombre de raies = = 320

et sans oublier la raie de fréquence zéro, nous obtiendrons 321 raies au total.

Dans le standard français à 625 lignes (dit CCIR L), la fréquence vidéo maximum est de 6 MHz, et nous aurons donc 384 + 1 soit 385 raies au total.

4) Modulation de l’onde porteuse – spectre total

Si nous désirons maintenant moduler une onde porteuse f par cette vidéo, nous obtiendrons comme à l’habitude un spectre complexe formé de nombreuses raies groupées autour de la fréquence porteuse f. La (figure 27) représente un tel spectre.

Remarque importante :

Observez bien les spectres des (figure 26) et (figure 27) . Vous remarquerez que les différentes raies ne se rejoignent pas. Il existe un emplacement vidéo où il n’y a pas de raies à 50 Hz.

C’est un fait extrêmement important et connu depuis 1934. A cette époque Mertz et Gray, deux techniciens américains, ont montré mathématiquement, que l’on pouvait placer dans ces intervalles vides, un autre spectre, totalement différent à condition que sa fréquence de répétition soit la même. Ces deux spectres peuvent donc coexister ensemble.

La (figure 28) représente une portion agrandie de l’intervalle compris entre deux raies à fréquence lignes accompagnées de leurs raies à 50 Hz et un spectre de raies étrangères (dessinées en pointillé). Comme vous pouvez le constater, les différentes raies se trouvent parfaitement localisées et coexistent sans se chevaucher.

La condition essentielle pour que ceci soit réalisé, est que le spectre étranger tombe exactement au milieu de deux raies distantes elles mêmes de 15 625 Hz, c'est-à-dire que le spectre parasite soit du à la modulation d’une onde porteuse dont la fréquence soit égale à un multiple impair de la demi fréquence lignes.

f = (2 k + 1)

Nous avons vu précédemment qu’un signal parasite à fréquence assez élevée se comportait comme un brouilleur et que sa visibilité sur l’écran du cathoscope se traduisait par un pointillé de l’image. On peut donc considérer maintenant son spectre.

Ce signal sinusoïdal est interrompu périodiquement à la fin de chaque balayage lignes et à la fin de chaque balayage images. Son spectre sera donc composé de raies qui se trouveront à l’intérieur du spectre vidéo normal.

Si la fréquence du signal parasite est bien égale à un nombre impair de fois la demi fréquence lignes, nous avons vu que les deux spectres peuvent s’intercaler parfaitement et c’est à cette condition que la visibilité du pointillé est la plus faible. En effet, dans ce cas :

f = (2 k + 1)

Le pointillé produit sur l’écran est immobile donc moins gênant qu’un pointillé mobile. D’autre part, grâce à l’inter calage exact des spectres, les effets de visibilité s’opposent et se détruisent en partie.

On peut donc en définitive voir ce problème sous deux aspects différents et dire :

Un signal parasite visible sur l’écran d’un tube cathoscope possède un spectre qui se trouve à l’intérieur du spectre vidéo normal.

Un spectre intercalé parfaitement (ou imparfaitement) à l’intérieur d’un spectre vidéo normal, se traduira sur l’écran d’un cathoscope par un pointillé plus ou moins visible.

Nous avons vu une notion essentielle, celle des spectres intercalés. Tous les systèmes de télévision en couleurs actuels exploitent cette propriété.

Or, les différents procédés de télévision en couleurs que nous avons examinés jusqu’à maintenant présentaient tous l’un des défauts suivants :

Ou bien ils n’étaient pas compatibles.

Ou bien la compatibilité n’était obtenue qu’au prix d’une grande complication du fonctionnement.

Les procédés simultanés que nous avons examinés au paragraphe B n’étaient pas compatibles puisqu’un récepteur noir et blanc ne pouvait exploiter qu’une seule des trois couleurs et aurait donc une image nettement moins bonne.

Les procédés séquentiels examinés au paragraphe C ne satisfaisaient pas non plus à la compatibilité, puisque certains utilisaient un standard de balayage différent du noir et blanc, et que même ceux qui n’avaient pas de défaut auraient conduit à une modification importante des récepteurs noir et blanc pour leur permettre d’utiliser les trois images transmises.

Le procédé des MIXED HIGHS que nous avons vu au paragraphe E n’étaient pas non plus réellement compatible puisqu’en ce qui concerne les basses fréquences, un récepteur noir et blanc n’aurait reçu que l’image verte.

Enfin, le procédé des points intercalés, que nous avons vu au paragraphe E, était bien compatible, mais cette compatibilité était obtenue au moyen d’artifices de circuits qui se sont révélés trop chers et trop difficiles à régler, pour pouvoir être utilisés dans des récepteurs destinés à la fabrication en grande série et à aussi bas prix que possible.

G) Introduction aux procédés modernes de télévision en couleurs

C’est dans le texte des brevets déposés dès 1938 par l’ingénieur français Valensi que l’on trouve, pour la première fois, clairement définis les principes sur lesquels reposent les procédés modernes.

Dans un procédé de télévision en couleurs, il faut transmettre deux espèces de signaux différents :

Un signal rigoureusement identique à celui de la télévision en noir et blanc. Ce signal comportera donc évidemment les impulsions de synchronisation et le signal vidéo normal. L’information que transporte ce signal vidéo est la luminance de la scène télévisée, à l’exclusion de toute information de couleur. De cette manière, les deux conditions de compatibilité seront automatiquement réalisées, puisque le récepteur noir et blanc pourra utiliser directement ce premier signal et que, d’autre part, le récepteur couleur, prévu pour recevoir ce signal, n’éprouvera aucune difficulté à utiliser une émission en noir et blanc.

Un signal de chrominance apportant au récepteur couleur les informations nécessaires pour colorier l’image fournie par le premier signal. Ce deuxième signal doit transporter uniquement des informations sur la couleur et aucune sur la luminance. Il n’est pas reçu par le récepteur noir et blanc, mais encore faut il qu’il ne perturbe pas son fonctionnement.

C’est par les moyens utilisés pour transmettre ce signal de chrominance que les différents procédés de télévision en couleurs se distinguent les uns des autres.

A ce stade, nous devons faire une remarque importante : nous avons vu au paragraphe F que dans le spectre vidéo d’une émission en noir et blanc (donc dans le spectre du signal de luminance en télévision en couleurs), il existe des espaces vides qui permettent, moyennant certaines précautions, d’intercaler un autre spectre pratiquement sans nuire à la qualité de l’image.

C’est donc ce procédé qui sera utilisé pour transmettre le signal de chrominance, ce qui nous permet d’ajouter aux deux conditions de compatibilité la troisième condition suivante : la largeur totale du spectre d’une émission de télévision en couleurs doit être exactement la même que celle d’une émission en noir et blanc.

Le respect de cette condition permet, au moins en théorie, d’utiliser pour les liaisons entre studios et émetteurs, l’énorme infrastructure de câbles et relais hertziens existants déjà pour le noir et blanc.

1) Procédé Valensi

Dans ce système, on distingue un signal de luminance et un signal de chrominance.

Le signal de luminance identique à celui de la télévision en noir et blanc, module directement en amplitude la porteuse image de l’émetteur.

Le signal de chrominance est obtenu de façon très particulière : Valensi a découpé dans le triangle XYZ des couleurs 52 secteurs, correspondant à des couleurs discernables par l’œil. Il a numéroté ces secteurs de 0 à 51, comme l’indique la (figure 29) .

L’information de couleur est représentée par la valeur d’une tension électrique proportionnelle au numéro du secteur. Le signal ainsi obtenu, à bande étroite, module en amplitude une sous porteuse qui est intercalée dans le spectre du signal de luminance.

Ce procédé n’étant plus d’actualité, nous ne nous étendrons pas sur la méthode utilisée pour obtenir le signal de chrominance : disons seulement qu’elle utilisait des tubes cathodiques spéciaux, ce qui était un défaut du système.

Un autre défaut était d’ailleurs la mauvaise définition de la couleur, 52 secteurs ne suffisant pas pour rendre compte de toutes les nuances discernables par l’œil.

Mais l’intérêt du procédé est de bien montrer comment les signaux de luminance et de chrominance peuvent être totalement séparés.

2) Prise de vue des images colorées

a) Notions de gamma d’un tube

Supposons que le signal électrique, issu du tube analyseur, est amplifié par une chaîne d’amplificateurs dont la sortie attaque le canon correspondant du tube reproducteur.

En général, le courant i de sortie du tube analyseur n’est pas rigoureusement proportionnel à la brillance B de l’image analysée. Il est donné par la formule :

i = k . B où k est un coefficient dépendant du tube analyseur et est un nombre généralement inférieur à 1 appelé le gamma du tube. Si était égal à 1, le courant i serait proportionnel à B (figure 30) .

De même, la brillance B de l’image reproduite par le tube de réception n’est généralement pas proportionnelle à la tension V de sortie de l’amplificateur (appliquée au canon du tube), mais est donnée par :

B = k’ V où k’ coefficient dépendant du tube cathodique et est le gamma du tube de réception.

Il s’ensuit que, si l’amplificateur est linéaire, c'est-à-dire si V est proportionnel à i, B, brillance reproduite n’est pas proportionnelle à B, brillance d’origine, mais à :

(B ) = B

Si par exemple = 0,9 et = 2,2 (valeurs que l’on rencontre fréquemment) . 2 et B est proportionnel à , ce qui constitue une erreur de reproduction importante.

Il est donc nécessaire d’intercaler dans la chaîne d’amplificateur un circuit correcteur tel, qu’on ait :

V = k’’ . i en choisissant : =

On aura alors B proportionnel à B . .

Pour simplifier les récepteurs, ce circuit correcteur est incorporé dans l’émetteur, ce qui veut dire que la porteuse de l’émetteur devra être modulée par une tension vidéo proportionnelle à :

(B) , étant le gamma du tube récepteur. En général, est voisin de 2.

b) Tubes analyseurs utilisés dans les caméras trichromes

Dans le chapitre 1, les tubes analyseurs Orthicon, Vidicon et Plumbicon ont été largement décrits. Précisons simplement que le tube Orthicon a un gamma de l’ordre de 1 et le tube Vidicon de l’ordre de 0,6.

Voyons maintenant deux autres tubes et d’abord le tube Tiam.

La (figure 31) donne son principe de fonctionnement. L’image optique est formée sur la photocathode. Des électrons, plus ou moins nombreux suivant l’éclairement, quittent la photocathode et tombent sur la cible, sur la face externe de laquelle se forme une image électrostatique.

Sur l’autre face de la cible (côté cathode) se forme la même image électrostatique mais en négatif. Le faisceau d’analyse, en bombardant le point examiné, extrait un nombre plus ou moins grand d’électrons secondaires, qui sont recueillis sur une anode collectrice et provoquent aux bornes de la résistance de sortie, le signal vidéo proprement dit.

Les images obtenues sont excellentes et le rapport signal sur bruit est supérieur à tous les autres tubes connus jusqu’à ce jour.

Le tube Tiam est de dimensions légèrement supérieures à celles du Vidicon. Son gamma est aussi de l’ordre de 1.

Tube analyseur Flying Spot

Ce dispositif est essentiellement utilisé pour l’analyse d’images fixes, diapositives par exemple. Le fonctionnement du Flying Spot est plus simple que celui de tous les tubes analyseurs que nous avons vus jusqu’ici.

En effet, au lieu d’éclairer la cible par l’intégralité de la scène à analyser et de balayer la cible, on éclaire successivement chaque point de la scène à analyser. La lumière réfléchie par la photo ou recueillie au travers de la diapositive est dirigée sur toute la surface de la cible d’une cellule photo électrique.

La source de lumière est un tube cathodique à faible rémanence. Le spot doit être très brillant et très fin. Le balayage doit être effectué avec une lumière parfaitement uniforme sur tout l’écran. Pour l’analyse des scènes en noir et blanc, la couleur de la lumière d’analyse se situe dans le violet. Ceci est obtenu avec des poudres luminescentes à base de sulfure de zinc ou bien de silicate de calcium et de magnésium. Pour l’analyse des scènes en couleurs, la lumière du tube cathodique doit être blanche afin de ne pas favoriser certaines couleurs.

Le fonctionnement du Flying Spot est le suivant, ainsi que le représente la (figure 32) .

Le spot produit par le tube cathodique est concentré par l’objectif S1 sur la diapositive qu’il explore. La lentille S2 qui recueille la lumière modulée par la diapositive éclaire la cellule photo électrique qui délivre le signal vidéo. La cellule photo électrique est avantageusement remplacée par un photomultiplicateur dont la sensibilité est de 50 à 500 A/1m et dont le rapport signal/bruit est bon (30 à 40 dB).

L’analyse d’une diapositive pour la télévision en couleurs s’effectue selon le même principe. Un système optique à miroir semi transparent envoie les trois composantes modulées de la lumière sur trois photomultiplicateurs comme le représente la (figure 33) .

Les signaux vidéo délivrés pour les photomultiplicateurs doivent subir une correction en gamma à l’instar des tubes analyseurs classiques mais également une correction de traînage et de définition.

Compte tenu du gamma des photos et des diapositives de l’ordre de 1 à 1,3, la correction de gamma à appliquer est de l’ordre de 0,5 pour les Flying Spot trichromes.

La correction de traînage est rendue nécessaire à cause de la rémanence du tube cathodique et du déplacement rapide du spot qui a la forme d’une goutte d’eau très effilée. On corrige ce défaut en appliquant le signal différenciateur dont la constante de temps est égale à celle du défaut. On obtient ainsi un signal dont la forme est, mathématiquement, la dérivée première du signal original.

Les dimensions non nulles du spot d’analyse rendent nécessaires la correction de définition. Ce défaut est partiellement corrigé en superposant au signal d’origine, un signal qui est obtenu à partir du signal original. Ce signal ajouté est mathématiquement l’inverse de la dérivée seconde du signal original.

c) Télécinéma à Flying Spot

Nous avons vu, au chapitre précédent, la technique du Flying Spot pour l’analyse d’images fixes. Nous allons maintenant voir comment ce système permet la diffusion de films donc l’analyse d’images animées.

La (figure 34) représente le principe d’un télécinéma Flying Spot.

Un tube cathodique à faible rémanence produit un spot d’analyse de l’image. Un système optique constitué de deux lentilles forme deux spots à partir du spot du tube cathodique. Chaque spot est concentré sur le film qui défile au rythme d’une demi image pendant la durée de balayage d’une trame. Pendant une trame, un des deux spots arrive sur le film tandis que l’autre est masqué par un obturateur.

A la trame suivante, l’obturateur commute les spots, celui qui était masqué arrive sur le film et l’autre se trouve masqué.

Voyons maintenant comment s’effectue l’analyse du film.

Pendant la première trame, le tube cathodique est balayé sur la moitié de sa hauteur dans le sens haut bas.

Pendant cette phase, l’obturateur est devant la lentille P2 et seul le spot concentré par la lentille P1 est actif. Cette lentille est disposée de telle manière que, pendant cette même phase, le spot la traversant, balaie de bas en haut la moitié de l’image (1) du film supposé fixe pour le moment (figure 35 a et b) .

Si l’on imprime simultanément à ce film un mouvement de haut en bas à la vitesse de ½ image par trame, le spot traversant P1 aura alors balayé une image complète (1) du film pendant le balayage de la moitié supérieure de l’écran du tube cathodique (figure 35 c) .

A la fin de l’analyse de la première trame, le spot se trouvant à mi hauteur du tube cathodique, l’obturateur commute, masquant ainsi la lentille P1 et découvrant la lentille P2.

De part la position de la lentille P2, le spot se retrouve alors en bas de la première image (figure 36 a) .

C’est le début de l’analyse de la deuxième trame. Le spot balaie la deuxième moitié de l’écran du tube cathodique toujours dans le sens haut bas. Le film défile toujours à la vitesse d’une demi image par trame et ainsi l’image (1) est analysée en entier et pour la seconde fois pour permettre le système de balayage entrelacé. Arrivé à la configuration de la (figure 36 b) , l’image a été analysée par les deux trames et l’obturateur commute, revenant alors dans la position de la (figure 35 a) pour le début de l’analyse de la première trame de l’image (2). L’image (2) est à cet instant à la place de l’image (1) car le film se déroule en continu.

L’analyse d’un film couleur repose sur le même principe. La lumière recueillie est séparée par des miroirs dichroïques et dirigée à travers des filtres vers trois photomultiplicateurs comme le représente la (figure 33) pour l’analyse d’images fixes.

d) Les caméras pour prise de vue en télévision couleurs

Nous avons vu, en colorimétrie, qu’il était possible de reproduire presque n’importe quelle couleur de la nature, par synthèse additive trichrome.

Si l’on désire donc transmettre une image en couleurs, il suffit de la décomposer en trois images dans les couleurs primaires, d’analyser ces trois images séparément par trois caméras identiques, de véhiculer ces trois signaux vidéo et de superposer à la réception en excitant les trois canons d’un tube cathoscope trichrome.

Les trois couleurs fondamentales R,G et B ont été déterminées de façon à couvrir une surface de couleurs maximum (figure 37) . Elles ont pour coordonnées :

Rouge : x = 0,67 y = 0,33

Vert : x = 0,21 y = 0,71

Bleu : x = 0,14 y = 0,08

Blanc illuminant C : x = 0,310 y = 0,316

Les coordonnées choisies sont les mêmes pour tous les systèmes de télévision actuels.

Seules, les couleurs à l’intérieur de triangle R G B voir (figure 37) , peuvent être reproduites. Si l’on avait à reproduire la couleur du point P’ par exemple, on ne pourrait évidemment pas le faire, et seul le point P serait transmis (couleur un peu dé saturée par rapport à P’).

Dans les caméras trichromes, l’image directe est divisée en trois images à l’aide de miroirs semi transparents sur le trajet desquels des filtres de sélection, permettent d’obtenir les trois couleurs primaires (figure 38) .

Quelques fois, les filtres de sélection sont inutiles lorsque les miroirs semi transparents sont remplacés par des miroirs dichroïques qui effectuent la sélection eux-mêmes.

Les filtres de sélection (ou les miroirs dichroïques) sont réalisés de telle façon que les trois couleurs primaires se trouvent exactement aux points indiqués sur la (figure 37) . La courbe de réponse de ces filtres est de la forme représentée (figure 39) .

La séparation optique a permis d’obtenir trois images de sélection : chaque tube de la caméra trichrome analyse pour son propre compte son image de la même façon qu’une caméra noir et blanc.

Le problème le plus important est que les signaux doivent être parfaitement synchrones de façon que les images puissent être superposables à la réception.

Cette nécessité de superposition des images entraîne à choisir des caméras les plus semblables possible, de façon à assurer dans chaque voie une symétrie parfaite.

Les tubes et les bobinages de déflexion devront avoir les mêmes caractéristiques. Les objectifs devront être semblables. Les tolérances dans les composants électroniques ou mécaniques devront être serrées.

Les bobinages de déflexion sont excités, en général, en série.

Des réglages séparés sont de plus prévus, de façon à parfaire la coïncidence. La précision exigée est de 0,7%, si l’on désire avoir une qualité finale comparable au noir et blanc.

Comme vous pouvez le constater, ces problèmes de tolérance, de stabilité, de coïncidence sont difficiles à résoudre.

D’autre part, il est bien évident qu’une perte de lumière très grande, a lieu dans la division optique et dans le filtrage coloré. Le flux lumineux est d’abord partagé en trois. Ensuite, ce flux lumineux est filtré : perte de l’ordre de deux. Ceci fait donc une perte globale de 6 environ.

L’éclairage des plateaux des studios de télévision en couleurs, devra donc être 5 à 6 fois plus grand que pour le noir et blanc.

e) Caméras de prise de vue en Flying Spot

Le tube cathodique sue lequel se forme la trame de télévision, comporte un écran phosphorescent blanc.

Le film couleurs est donc analysé par un spot blanc. Derrière l’objectif, une division optique suivie d’un filtrage coloré, revoie les trois faisceaux primaires sur trois cellules qui délivrent directement les trois signaux vidéo.

f) Caméras à trois tubes Vidicon

Ces caméras sont utilisées surtout pour analyser les films couleurs ou des images fixes et ce concurremment avec les caméras Flying Spot. L’inconvénient est que pour limiter le traînage, l’éclairement de la scène doit être important : 5 000 à 6 000 lux sont souvent nécessaires.

La caméra est de dimensions réduites, d’où le principal avantage (15 kg environ).

g) Caméras à trois tubes Plumbicon

Ces caméras permettent des prises de vue en extérieur et l’éclairement nécessaire est de l’ordre de 1500 lux.

h) Caméras à trois tubes image Orthicon

C’est le type de caméras le plus utilisé actuellement, car les tubes sont sensibles et un éclairage de 2 000 lux est suffisant pour une bonne profondeur de champ.

Le seul inconvénient est que ces caméras sont lourdes et encombrantes (200 kg environ), ce qui limite leur emploi aux seules prises de vue en intérieur.

i) Caméra à luminance séparée

Toutes les caméras que nous avons examinées jusqu’ici, travaillent sur le principe d’analyse séparée des trois couleurs primaires. Le signal de luminance est alors obtenu par addition pondérée des trois signaux de couleurs.

Mais on peut également envisager d’obtenir directement le signal de luminance au moyen d’un tube Orthicon à haute définition et les signaux rouge et bleu au moyen de deux tubes Vidicon donc beaucoup plus légers mais à moins bonne définition, et précédés de filtres rouge et bleu.

Il nous faut ouvrir ici, une parenthèse. En effet, nous parlons de signaux rouge et bleu mais pas du signal vert. Or, nous avons vu, en colorimétrie qu’une lumière ou image blanche peut être synthétisée par addition des trois couleurs primaires bleu + rouge + vert.

La caméra à luminance séparée délivre, d’une part, le signal Y de luminance qui est la somme de trois images rouge, bleu et vert, et d’autre part, un signal bleu et un signal rouge. Nous voyons donc que bien que l’information verte ne soit pas transmise individuellement, on peut la restituer.

Il suffit en effet, de soustraire à la réception du signal de luminance Y, les deux signaux rouge et bleu.

On obtient alors : (R + G + B) – (R + B) = G

Les caméras pourraient aussi exploiter ce principe. Un tube analyseur d’excellente qualité, à haute définition délivrerait le signal achrome (noir et blanc) compatible. Le signal de luminance sera analysé par un tube image Orthicon.

Le signal délivré par l’amplificateur linéaire qui suit le tube sera donc une tension électrique que nous pouvons écrire Y.

Les sélections couleurs rouge et bleu seront analysées par deux tubes Vidicon (gamma = 0,6).

Après correction du gamma (pré distorsion de ), on obtiendra les signaux électriques que nous écrirons R et B.

Après avoir réalisé les signaux (R – Y) et (B – Y) dans une matrice, les signaux de chrominance pourront moduler les deux sous porteuses.

Obtention du signal de chrominance R –Y ou B – Y

Le signal Y ayant été obtenu (directement par un tube image Orthicon ou par addition pondérée des trois primaires), est envoyé dans un inverseur de phase : par exemple sur la base d’un transistor dont le gain est de 1 : le signal (- Y) est récupéré sur le collecteur du transistor.

Les deux signaux à additionner R et (- Y) sont alors ajoutés dans une résistance de charge commune R. Les résistances de protection R servent à découpler les sources (- Y) et (R) de façon à supprimer les inter actions possibles (figure 40) .

Obtention du signal de luminance Y

Le signal de luminance Y peut être composé à l’aide d’un mélange additif pondéré des trois signaux primaires. Nous allons voir, dans quelles proportions :

j) Proportion des couleurs primaires dans le signal Y

La sensibilité de l’œil humain aux couleurs primaires n’est pas identique. L’œil est très sensible au vert, moins sensible au rouge et très peu sensible au bleu.

A la suite de tests sur un large échantillon d’individus, il a été établi statiquement la courbe de sensibilité relative de l’œil humain.

La visibilité relative au vert est de 0,9, de 0,46 au rouge et de 0,17 au bleu.

En télévision couleurs, une image blanche étant la somme de ces trois couleurs, on peut donc calculer la proportion de chacune des primaires dans le signal de luminance Y.

Pour le vert on aura :

x 100 = 59% de vert ou 0,59

Pour le rouge :

x 100 = 30% de rouge ou 0,30

Pour le bleu :

x 100 = 11% de bleu ou 0,11

Il suffit alors d’additionner les trois signaux ainsi réduits, pour former le signal de luminance Y :

Y = 0,30 R + 0,59 G + 0,11 B (figure 41)

3) Principe de la luminance constante

Nous venons de voir l’intérêt de transmettre séparément les signaux de luminance et les signaux de chrominance.

Ce principe est dit à luminance constante, on devrait d’ailleurs plutôt dire à luminance séparée, terme plus exact à notre avis.

Tous les systèmes de télévision en couleurs modernes utilisent ce principe de manière identique.

Le signal de luminance Y est défini par l’équation :

Y = 0,30 R + 0,59 G + 0,11 B où les signaux R,G et B sont les signaux primaires délivrés par la caméra trichrome.

Le signal de luminance est transmis, rappelons le, à large bande de façon à bien reproduire les détails fins.

Ce signal sert aussi dans les récepteurs noir et blanc à la restitution de l’image achrome habituelle (compatibilité).

Les signaux de couleur, eux, sont transmis sous forme des différences ( R –Y ), ( B - Y) et ( G - Y) (reconstitués dans le récepteur) et nous avons vu qu’ainsi, ils ne participent pas à la luminance de l’image.

Cela veut dire qu’une perturbation affectant ces signaux de couleur ne modifie pas la luminance de l’image reproduite, mais modifie seulement sa couleur : c’est la le principal intérêt de la transmission à luminance constante.

Nous avons vu au paragraphe G, que les tubes reproducteurs actuellement disponibles présentaient une caractéristique tension de commande – lumière émise non linéaire.

Ceci provient de la nature même des canons électroniques utilisés dans la commande des faisceaux d’électrons : la brillance du spot, en fonction de la tension de commande s’écrit donc :

B = k . V , est le gamma du tube reproducteur.

Les tubes récepteurs actuellement utilisés en télévision couleurs, ont un gamma de l’ordre de 2 (2,2 exactement).

Nous savons donc, que nous aurons à prévoir des circuits de correction non linéaire, en sens inverse, de façon à compenser cette non linéarité du tube récepteur.

La (figure 42 a) indique la caractéristique d’un tube trichrome classique.

La correction en sens inverse que l’on devra prévoir devra affecter la forme donnée par la (figure 42 b) .

Les deux caractéristiques se compensant mutuellement, la réponse finale sera linéaire (figure 42 c) .

Le circuit de correction peut être placé pratiquement en n’importe quel point de la chaîne de transmission. L’emplacement le plus simple, est évidemment dans la chaîne d’émission.

Il suffit, pour cela, que le gamma de tous les récepteurs soit le même, ce qui est vrai en pratique. En télévision en noir et blanc, cette pratique de correction est universellement adoptée.

On pourrait placer le circuit de correction dans les récepteurs : l’inconvénient majeur est le prix de revient, chaque récepteur devrait comporter un correcteur, tandis qu’avec la correction à l’émission, seuls les émetteurs en sont équipés.

Le problème est donc simple, en ce qui concerne la télévision en noir et blanc : la correction se fait à l’émission.

Le problème se complique beaucoup en télévision en couleurs. En télévision en couleurs, nous avons affaire à trois signaux qui sont les informations rouge, verte et bleue. Les signaux électriques dont on doit disposer à la réception sont :

R, B et G , on a pris l’habitude de désigner ces signaux en mettant un « prime » aux signaux R, G et B, nous écrirons donc :

R’ = R - G’ = G - B’ = B , nous dirons que les signaux R’, G’ et B’ sont les signaux corrigés en gamma et nécessaires à la réception. Les signaux corrigés R’, G’ et B’ sont très facilement obtenus à l’émission, par correction en gamma de chaque signal d’image primaire (figure 43) .

Pour le signal de luminance, de la même manière, après avoir obtenu le signal :

Y = 0,30 R + 0,59 G + 0,11 B

Nous devrions transmettre dans la voie de luminance, le signal corrigé en gamma : L’ = Y.

Or, nous avons vu tout à l’heure, que la transmission des signaux de chrominance s’effectuait sous la forme différence R – Y et B – Y .

En réalité, ce sont les signaux primes, corrigés en gamma, que l’on transmet.

Si l’on transmet le signal de luminance sous la forme L’, on doit pouvoir écrire la relation Y = 0,30 R + 0,59 G + 0,11 B sous la forme 0,30 (R’ – L’) + 0,59 (G’ – L’) + 0,11 ( B’ – L’) = 0 puisqu’on a le signal Y’ sous la forme de la somme pondérée des trois primaires moins le signal luminance corrigé en gamma.

Voyons si cette relation est juste :

0,30 R’ – 0,30 L’ + 0,59 G’ – 0,59 L’ + 0,11 B’ – 0,11 L’ = 0

0,30 R’ + 0,59 G’ + 0,11 B’ – ( 0,30 L’ + 0,59 L’ + 0,11 L’) = 0

Y’ – L’ = 0

Donc Y’ – L’ 0 ce qui démontre que cette relation est fausse et qu’il ne faut donc pas utiliser L’. On va donc transmettre Y’ qui est obtenu en faisant la somme des primaires corrigés en gamma :

Y’ = 0,30 R’ + 0,59 G’ + 0,11 B’

Or, nous avons vu, tout à l’heure, que la transmission des signaux de chrominance s’effectuait sous la forme différence R – Y et B – Y.

En réalité, ce sont les signaux primes, corrigés en gamma, que l’on transmet. Si l’on transmet le signal L’ qui est le signal Y corrigé en gamma, on doit pouvoir écrire la relation :

Y = 0,30 R + 0,59 G + 0,11 B sous la forme : 0,30 (R’ – L’) + 0,59 (G’ – L’) + 0,11 (B’ – L’) = 0

Puisqu’on a le signal Y’ sous la forme somme pondérée des trois primaires moins le signal luminance corrigé en gamma. La relation devient alors :

0,30 (R’ – Y’) + 0,59 (G’ – Y’) + 0,11 (B’ – Y’) = 0

0,30 R’ – 0,30 Y’ + 0,59 G’ – 0,59 Y’ + 0,11 B’ – 0,11 Y’ = 0

0,30 R’ + 0,59 G’ + 0,11 B’ – ( 0,30 Y’ + 0,59 Y’ + 0,11 Y’) = 0

Y’ – Y’ = 0 ce qui est juste.

Mais nous avons transmis un signal Y’ différent du signal L’ que nous aurions voulu. Voyons d’abord en quoi ces deux signaux diffèrent.

a) différence entre L’ et Y’

Le premier est obtenu en ajoutant d’abord les signaux primaires et en corrigeant ensuite le tout, le second en corrigeant d’abord les signaux primaires, puis en les sommant seulement après.

Prenons un exemple numérique simple pour mieux comprendre et évaluer les différences. Soit les signaux délivrés par la caméra trichrome :

R = = 0,333, G = = 0,5 , B = = 0,25

Premier cas – transmission de L’

Y = 0,30 R + 0,60 G + 0,10 B (nous prenons 0,60 G au lieu de 0,59 G et 0,10 B au lieu de 0,11 B pour simplifier les calculs) :

Y = (0,30 x ) + (0,60 x ) + ( 0,10 x )

Y = 0,10 + 0,30 + 0,025 = 0,425

Nous avons vu que le gamma du tube récepteur était de l’ordre de 2,2.

Pour simplifier les calculs, nous prendrons = 2 , d’où la luminance L’ corrigée :

L’ = Y = Y = = = 0,652

L’ = 0,652

Deuxième cas – correction des signaux R, G et B d’abord, puis sommation des résultats (obtention du signal Y’)

Les signaux R, G et B après correction deviennent :

R’ = R = R =

De même :

G’ = , B’ = , R’ = = 0,576 , G’ = = 0,707

B’ = = 0,5

Le signal de luminance après correction est donc :

Y’ = 0,30 R’ + 0,60 G’ + 0,10 B’

Y’ = (0,30 x 0,576) + (0,60 x 0,707) + (0,10 x 0,5)

Y’ = 0,1728 + 0,4242 + 0,05

Y’ = 0,647

Y’ est inférieur à la luminance L’ vraie.

Le signal Y’ est toujours plus faible que L’ dans le cas d’une image en couleurs.

Le signal théorique L’ et le signal pratique Y’ sont égaux pour les plages blanches, grises ou noires.

1) dans le cas d’une plage noire, on a :

R = G = B = 0 d’où :

L’ = (0,30 R + 0,59 G + 0,11 B = (0 + 0 + 0) = 0 et

Y’ = 0,30 R’ + 0,59 G’ + 0,11 B’ or

R’ = R = 0 = 0 de même G’ = B’ = 0 et Y’ = 0

On a donc bien : L’ = Y’

2) Dans le cas d’une plage blanche, on a :

R = G = B = 1

L’ =

L’ =

L’ = 1 = 1 L’ = 1 et

Y’ = (0,30 x 1) + (0,59 x 1) + (0,11 x 1) = 1 Y’ = 1

Car 1 = 1 on a donc encore une fois L’ = Y’

3) Dans le cas d’une plage grise

Nous savons que les signaux R, G et B sont égaux et compris entre 0 et 1, écrivons que :

R = G = B = k avec 0 < k < 1 d’où

L’ = (0,30 k + 0,59 k + 0,11 k)

L’ = L’ = k

Et la luminance pratique Y’ sera :

Y’ = 0,30 k + 0,59 k + 0,11 k

Y’ = k (0,30 + 0,59 + 0,11) Y’ = k

On a donc bien : L’ = Y’

b) Conséquences pour un récepteur noir et blanc de la transmission du signal Y’

Le récepteur noir et blanc utilise le seul signal Y’.

Donc, c’est seulement dans les parties non colorées de l’image (plages blanches, grises ou noires) que les brillances reproduites par les récepteurs noir et blanc sont parfaitement correctes.

Par contre, les plages colorées de l’image sont reproduites sur le récepteur noir et blanc avec une luminance plus faible que normale.

Heureusement, l’expérience montre que les écarts obtenus avec les couleurs les plus courantes sont faibles et pratiquement invisibles.

L’écart au principe de la luminance constante affecte donc en premier lieu les récepteurs noir et blanc, mais l’inconvénient qui en résulte est faible et pourra être négligé.

c) Conséquences pour un récepteur couleurs de la transmission du signal Y’

Le récepteur couleurs, lui, utilise les trois signaux Y’, (R’ – Y’), (B’ – Y’) pour calculer d’abord (G’ – Y’) , puis R’, G’, B’, qui sont les trois signaux nécessaires pour reproduire une image colorée parfaite, aussi bien en luminance qu’en couleurs, comme le montre la (figure 44) .

La réception en couleurs semblerait donc n’avoir aucun défaut. Pourtant, comme le récepteur achrome, le récepteur couleurs a reçu un signal de luminance pratique Y’ qui est toujours inférieur, pour les plages colorées, au signal de luminance vraie L’.

C’est donc qu’une partie de la luminance du sujet qui sera transmise par les signaux de couleurs (R’ – Y’) et (B’ – Y’).

Or, c’est précisément ce que l’on voulait éviter, car on s’écarte du principe qui voulait assurer l’indépendance du canal de luminance vis-à-vis des informations de couleurs.

Nous avons dit que les signaux couleurs pouvaient varier dans certaines limites sans que ces fluctuations deviennent visibles, à la condition expresse qu’elles n’affectent pas la brillance de l’image.

Malheureusement, c’est ce qui se produit ici : les distorsions se produisant sur les signaux couleurs, les fluctuations affectant ceux ci lors de la transmission, vont se traduire par une visibilité accrue, car ils vont affecter non seulement la chromaticité, mais aussi la brillance.

Ce défaut est d’autant plus marqué que le rapport :

k = est plus petit.

La (figure 45) nous montre, dans le triangle des couleurs, les courbes (en pointillé) correspondant à diverses valeurs de k, et les valeurs de k pour certains points situés sur le triangle, donc correspondant à des couleurs saturées.

Vous voyez que k est d’autant plus petit, que la couleur est plus saturée.

Ainsi donc, la contribution qu’apportent les signaux de chrominance à la brillance, est d’autant plus grande (donc plus gênante) que les couleurs sont plus saturées.

Or, les couleurs saturées se rencontrent rarement dans la nature (de nombreuses expériences l’ont montré).

L’indice k reste donc proche de l’unité et le principe de luminance constante est assez bien respecté.

Compte tenu des inconvénients que nous venons de voir, on peut se demander s’il ne serait pas possible de transmettre le signal L’, luminance vraie, au lieu du signal Y’.

Si l’on transmet le signal de luminance exact L’ et les signaux de différence (R’ – L’) et (B’ – L’), on pourra obtenir très facilement les signaux de couleurs R’ et B’.

( R’ – L’) + L’ = R’ (B’ - L’) + L’ = B’

Mais on ne pourra plus obtenir directement le signal G’.

Il faudrait pour cela, à partir du signal L’, obtenir à nouveau le signal Y (donc nécessité d’avoir un circuit non linéaire). Ayant obtenu Y, il faudrait en déduire le signal G par la relation :

G =

Mais, comme vous pouvez le voir, on ne possède pas les signaux R et B mais les signaux R’ et B’. Il faudrait donc envoyer ces derniers signaux dans deux circuits, non linéaires, de façon à en extraire les informations R et B désirées.

Après avoir réussi à obtenir le signal G, il faudrait à nouveau le corriger en gamma (encore dans un circuit non linéaire) de façon à disposer du signal G’ désiré.

La (figure 46) indique les opérations qui seraient effectuées à l’émission, tandis que la (figure 47) indique celles qui seraient utiles à la réception.

La simple énumération des opérations, sans parler des circuits non linéaires nécessaires (toujours difficiles à réaliser, donc coûteux) montre le peu d’intérêt pratique qu’il y aurait à transmettre la luminance vraie L’.

Il y a évidemment la solution simple qui consiste à transmettre la luminance Y, non corrigée, et à effectuer la correction du gamma à la réception.

C’est la solution qui permettrait d’obtenir la luminance vraie, mais au prix de quatre correcteurs non linéaires à la réception.

Or, nous avons dit qu’il n’y avait jamais intérêt à corriger à la réception, d’abord à cause du prix, ensuite à cause des variations dans les tolérances des composants qui pourraient provoquer d’un récepteur à l’autre, des modifications dans les brillances et couleurs reproduites.

De plus, nous verrons plus tard que la transmission de signaux non corrigés en gamma est très défavorable du point de vue du rapport signal sur bruit.

La seule solution satisfaisante est donc la première examinée et universellement adoptée. Ce qui conduit aux synoptiques d’émission et de réception représentés (figure 48) ,que nous retrouverons dans les systèmes de télévision en couleurs exploités actuellement et entre autre, le procédé NTSC que nous allons examiner maintenant.

II – Procédé NTSC

Le premier système normalisé aux USA, le système CBS de transmission simultanée, ayant essuyé un échec complet, il fallut d’urgence trouver autre chose.

Les principaux constructeurs américains se sont donc associés au sein du NTSC (National Télévision Systèm Commitee = Comité National pour un Système de Télévision).

Cet organisme, doté de moyens d’étude puissants, s’attaqua à la mise au point d’un procédé réellement compatible, et après un travail remarquable, aboutit au système qui porte son nom, et qui fut mis en exploitation avec succès aux USA des le début de 1954.

A) Principe

Nous avons vu que le signal de chrominance (constitué en réalité par trois signaux de couleurs) ne doit transmettre aucune information de lumière (ou de luminance).

Or, si nous transmettons simplement les trois signaux R, G, B, ils contiennent une information de luminance, en effet, nous avons vu que Y = 0,30 R + 0,59 G + 0,11 B.

On tournera cette difficulté en transmettant, au lieu des signaux R, G et B, les signaux R – Y, G – Y et B – Y. Chacun de ces signaux est obtenu en retranchant de la valeur du signal de couleur (R par exemple), la valeur du signal de luminance Y obtenue précédemment. On peut vérifier ainsi que la luminance transmise par le canal de chrominance est nulle.

En effet, si nous appelons y cette luminance, on peut la calculer facilement en appliquant toujours la même formule :

y= 0,30 (R – Y) + 0,59 (G – Y) + 0,11 (B – Y)

En effectuant les multiplications indiquées par les parenthèses, on obtient :

y = 0,30 R + 0,59 G + 0,11 B -

Mais : 0,30 R + 0,59 G + 0,11 B = Y et 0,30 + 0,59 + 0,11 = 1 donc

y = Y – Y = 0

De cette manière, les signaux de chrominance ne transmettent donc aucune information de luminance.

Puisque, comme nous l’avons vu, 0,30 + 0,59 + 0,11 = 1, on peut écrire :

(0,30 + 0,59 + 0,11) Y = 0,30 R + 0,59 G + 0,11 B ou encore :

0,30 (R – Y) + 0,59 (G – Y) + 0,11 (B – Y) = 0

Donc l’un des trois signaux R –Y, G – Y et B – Y peut être calculé au moyen des deux autres. Par exemple, on peut calculer G – Y et on obtient :

G – Y = - (R – Y) - (B – Y) = - 0,51 (R – Y) – 0,19 (B – Y)

Nous en concluons qu’il est absolument inutile de transmettre ces trois signaux, mais que deux suffisent, puisque par une opération très facile à réaliser par des circuits électroniques, nous pourrons toujours calculer la valeur du troisième dans le récepteur.

Pour des raisons que nous vous donnerons plus tard, on a choisi de transmettre les signaux (R –Y) et (B – Y) et de calculer (G – Y) dans le récepteur.

Vous vous rappelez, sans doute, nous en avons encore parlé à propos du procédé des Mixed Highs, qu’il n’est pas nécessaire de transmettre les signaux de couleur avec la même bande passante que les signaux de luminance.

L’œil n’étant pas sensible à la couleur des détails fins, mais seulement à la luminance, il suffit que le signal de luminance soit transmis avec toute la bande passante.

On fait donc passer les signaux R – Y et B – Y, avant de les émettre, dans deux filtres passe bas qui limitent leur spectre à 1 MHz environ.

De ce fait, le spectre du signal G – Y, qui est recalculé par le récepteur à partir des signaux R – Y et B – Y, sera lui aussi, limité à 1 MHz. Le récepteur n’est, en effet, pas capable de produire les fréquences élevées du signal G – Y, puisqu’on ne les lui fournit pas.

Il reste maintenant à incorporer les signaux de chrominance (R – Y) et (B – Y) dans le spectre du signal de luminance.

Vous savez déjà qu’il est possible de le faire en utilisant chacun de ces deux signaux pour moduler en amplitude une onde porteuse, et que la perturbation qu’apporteront ces porteuses sera très réduite si la fréquence de chacune d’elles est assez élevée et est en plus multiple impair de la demi fréquence de balayage lignes.

Une astuce supplémentaire permet encore de réduire la perturbation apportée par les porteuses : ces deux ondes porteuses ont exactement la même fréquence et ne se distinguent l’une de l’autre que parce que la deuxième est déphasée de 90° par rapport à la première. On dit alors qu’il s’agit de deux porteuses en quadrature.

Dans ces conditions, on peut parfaitement séparer à la réception les deux signaux véhiculés par ces deux porteuses, mais pour cela, il est nécessaire d’utiliser deux détecteurs synchrones pilotés par des oscillateurs rigoureusement en phase avec chacune des deux porteuses.

Pour obtenir ce résultat, on transmet pendant chaque retour entre les lignes de balayage 8 à 10 sinusoïdes (figure 49) de la fréquence de l’onde porteuse, qui seront utilisées à la réception pour synchroniser les oscillateurs de détection.

On appelle cela un color burst (littéralement : salve de couleurs). Ce color burst ne détériore en rien la qualité de l’image, puisqu’il est transmis pendant le retour, à un moment où le spot du cathoscope de réception est éteint.

Enfin, la porteuse est supprimée à l’émission, ce qui réduit encore le pointillé sur l’écran.

Avant d’examiner les signaux du procédé NTSC, voyons comment on peut réaliser une modulation d’amplitude à porteuse supprimée.

1) Modulateur à diodes

La (figure 50) représente un modulateur à diodes en treillis. Dans ce montage, la HF est appliquée au primaire du transformateur T1 et le signal modulant R – Y ou B – Y au primaire du transformateur T2

Ce signal est appliqué entre les points A et B du montage par le secondaire du transformateur T2. La HF modulée est recueillie au secondaire de T3.

Lorsque le signal modulant est nul, les points A et B sont au même potentiel. En conséquence, pendant l’alternance positive de la HF, les diodes D1 et D3 sont passantes et le secondaire de T1 se trouve ainsi court circuité, aucune tension n’apparaît sur le primaire de T3. Pendant l’alternance négative de la HF, les diodes D2 et D4 sont passantes et le secondaire de T1 est également court circuité, ce qui implique la même conséquence que précédemment. On constate donc qu’en absence de signal modulant, il y a absence de signal HF, la porteuse est supprimée lorsqu’il n’y a pas de modulation.

Voyons maintenant ce qui se passe quand un signal modulant tel que celui représenté à la (figure 51 b) , est appliqué au primaire de T2.

Durant la première alternance du signal modulant, le point A est positif par rapport au point B. Les diodes D1 et D2 sont passantes et les diodes D3 et D4 sont bloquées. La tension HF est transmise en phase au transformateur T3 avec une amplitude qui est en fonction de l’amplitude du signal modulant (figure 51 c) .

Durant la seconde alternance du signal modulant, le point A est négatif par rapport au point B. Les diodes D1 et D2 sont bloquées et les diodes D3 et D4 sont passantes. La tension HF est transmise en connexion croisée au primaire de T3 et on la retrouve donc en opposition de phase avec une amplitude qui est fonction de l’amplitude du signal modulant (figure 51 c) .

Nous avons donc réalisé une modulation avec suppression de porteuse. En effet, il n’y a pas d’onde porteuse quand le signal modulant est nul. Elle ne réapparaît que lorsque le signal modulant n’est plus nul.

Le spectre d’une telle modulation à porteuse supprimée, donc ne conservant que les bandes latérales est représenté à la (figure 52 b) , la (figure 52 a) représente le spectre d’une modulation d’amplitude normale sans suppression de porteuse.

B) Signaux de chrominance dans le système NTSC

1) Obtention des signaux R’ – Y’ et B’ – Y’

Le schéma de la (figure 53) montre comment on obtient, à partir des signaux électriques (tensions) délivrés par les trois tubes analyseurs, les signaux différence de couleur.

Les tubes analyseurs délivrent les tensions électriques R, G et B caractérisant la scène analysée. Ces signaux sont envoyés dans des circuits non linéaires correcteurs de gamma.

Les tensions à la sortie de ces correcteurs sont donc R’, G’ et B’ tel que :

R’ = R G’ = G B’ = B (avec )

Le signal R’ est ensuite atténué dans un rapport de 1 à 0,30 dans une matrice à résistances. Le signal G’ est réduit de 1 à 0,59 et B’ de 1 à 0,11.

Dans une matrice à résistances, on effectue l’addition de ces trois signaux réduits, et on obtient ainsi, le signal de luminance Y’.

Y’ = 0,30 R’ + 0,59 G’ + 0,11 B’

Ce signal est transmis à large bande ( 0 à 5 MHz pour le standard européen CCIR).

Le signal Y est inversé en phase, afin d’obtenir le signal (-Y’), puis dans une matrice à résistances, on effectue l’addition du signal R’ et du signal (- Y’).

Le signal de différence (R’ – Y’) est alors limité en bande dans un filtre passe bas à fréquence de coupure haute de 0,5 MHz. De même, on obtient le signal de différence (B’ – Y’).

2) Valeurs des signaux de différence dans quelques cas particuliers

a) Cas d’une plage blanche :

R’ = G’ = B’ = 1 volt

Les signaux de différence s’annulent :

(R’ – Y’) = 0 et (B’ – Y’) = 0

b) Cas d’une plage noire :

R’ = G’ = B’ = 0 on a évidemment :

(R’ – Y’) = 0 et (B’ – Y’) = 0

c) Cas d’une plage grise :

R’ = G’ = B’ = k avec 0 < k < 1 on a encore :

(R’ – Y’) = 0 et (B’ – Y’) = 0

d) Cas d’une plage rouge saturé :

R’ = 1 volt G’ = B’ = 0 Y’ = 0,30 volt donc :

(R’ – Y’) = 1 – 0,30 = 0,70 volt et (B’ – Y’) = 0 - 0,30 = - 30 volt

e) Cas d’une plage bleu saturé :

B’ = 1 volt R’ = G’ = 0 Y’ = 0,11 volt donc :

(R’ – Y’) = 0 – 0,11 = - 0,11 volt et (B’ – Y’) = 1 – 0,11 = 0,89 volt

f) Cas d’une plage vert saturé :

G’ = 1 volt R’ = B’ = 0 Y’ = 0,59 volt donc :

(R’ – Y’) = 0 – 0,59 = - 0,59 volt et (B’ – Y’) = 0 – 0,59 = - 0,59 volt

g) Cas d’une plage jaune :

Nous rappelons que le jaune est obtenu en mélangeant en proportions égales, du rouge et du vert.

On a donc : R’ = G’ = 1 volt B’ = 0 d’où : = 0,30 + 0,59 = 0,89 et :

(R’ – Y’) = 1 – 0,89 = 0,11 volt (B’ – Y’) = 0 – 0,89 = - 0,89 volt

h) Cas d’une plage bleu vert (cyan) :

B’ = G’ = 1 volt R’ = 0 d’où : Y’ = 0,59 + 0,11 = 0,70 volt et

(R’ – Y’) = 0 – 0,70 = - 0,70 volt (B’ – Y’) = 1 – 0,70 = 0,30 volt

i) Cas d’une plage magenta :

R’ = B’ = 1 volt G’ = 0 d’où : Y’ = 0,30 + 0,11 = 0,41 volt et :

(R’ – Y’) = 1 – 0,41 = 0,59 volt (B’ – Y’) = 1 – 0,41 = 0,59 volt

Nous nous sommes étendus délibérément sur le processus de formation des signaux dans quelques cas particuliers, car c’est le principe même qui est utilisé dans les générateurs de barres colorées.

Ces générateurs sont indispensables au technicien télévision couleurs au même titre que la mire en télévision noir et blanc.

La (figure 54) résume la situation. Pour chaque couleur particulière, nous vous donnons la valeur prise par le signal primaire correspondant (0 ou 1).

Ainsi, le signal de luminance varie évidemment de 0 (pour le noir) à 1 (pour le blanc), en passant par les valeurs particulières indiquées, il réalise donc à lui tout seul une véritable échelle de gris. Il est toujours positif.

Par contre, les signaux de différence prennent des valeurs tantôt positives, tantôt négatives, selon les couleurs à reproduire.

Remarquez que la disposition des différentes teintes n’a pas été faite au hasard.

En effet, avec la disposition adaptée, le signal R est une onde rectangulaire de fréquence double de la fréquence ligne, le signal B est de fréquence quadruple, tandis que le signal G est de même fréquence.

Ces signaux sont très facilement obtenus à partir de multivibrateurs classiques dans les mires de barres.

3) Formation du signal vidéo composite

Les signaux R’ – Y’ et B’ – Y’ modulent en amplitude à porteuse supprimée deux sous porteuses en quadrature mais de même fréquence.

Les deux sous porteuses modulées sont ensuite mélangées, on obtient ainsi le signal de chrominance qui est lui-même ajouté au signal de luminance qui donne le signal vidéo composite ainsi que le représente la (figure 55).

Nous avons donc en sortie du mélangeur de sous porteuse un signal de chrominance qui contient toutes les informations nécessaires à la reproduction correcte des couleurs. La phase de la sous porteuse détermine la teinte de la couleur transmise et l’amplitude donne la saturation.

4) Modulation en amplitude et en phase

Nous venons de voir que l’on module en amplitude deux sous porteuses en quadrature de phase. Dans la (figure 56) , les deux sous porteuses sont représentées sur l’axe x’ 0x pour la sous porteuse B’ – Y’ et sur l’axe y’ 0y pour la sous porteuse R’ – Y’. Considérons, par exemple, la sous porteuse B’ – Y’ représentée sur l’axe x’ 0x.

Si la modulation de cette sous porteuse est nulle, sa représentation est le point 0. Si la modulation est de 100%, la représentation de la sous porteuse est le vecteur (qui a pour module 1 et qui correspond à la couleur saturée).

Si la modulation de la sous porteuse de B’ – Y’ est de 50% que l’on représente par un vecteur de module égal à 0,5 et celle de R’ – Y’ de 50% également, le vecteur résultant fait alors un angle de 45° avec l’axe x’ 0x.

Ainsi, la modulation en amplitude des deux sous porteuses équivaut à la modulation et en phase d’une seule sous porteuse telle que le représente la (figure 56) . L’angle de ce vecteur donne la teinte et le module la saturation.

Le vecteur représente le signal transmis et il est donc important de connaître son amplitude et son angle de phase.

Le segment 0P est l’hypoténuse du triangle rectangle dont B’ – Y’ et R’ – Y’ sont les deux autres côtés.

D’après le théorème de Pythagore, nous avons donc :

0P = (R’ – Y’) + (B’ – Y’)

0P =

Pour déterminer l’angle , calculons sa tangente :

Soit tg =

Il suffit ensuite à l’aide d’une table ou d’une calculatrice, de rechercher la valeur de l’angle .

Voyons par exemple quelle est l’amplitude et la phase de la sous porteuse pour le rouge saturé : vecteur sur la (figure 56) .

La luminance Y’ vaut 0,30 R’ car B’ et G’ sont nuls, et puisque le rouge est saturé R’ = 1, donc R’ – Y’ = 1 – 0,30 = 0,70 et B’ – Y’ = 0 – 0,30 = - 0,30.

L’amplitude de la sous porteuse vaut donc :

0R =

On peut voir que le vecteur représentatif se situe dans le second quadrant car R’ – Y’ est positif et B’ – Y’ négatif. Calculons le déphasage :

tg = = - 2,333, on en déduit un angle de 113°.

En faisant de même pour les autres couleurs, on en déduit les valeurs indiquées dans le tableau de la (figure 57 a) .

La (figure 57 b) donne la représentation vectorielle de la sous porteuse pour ces diverses couleurs.

Les deux sous porteuses modulées par R’ – Y’ et B’ – Y’ sont représentées à la (figure 58 a et 58 b) .

On obtient le signal de chrominance représenté à la (figure 58 c) (valeurs arrondies) en mélangeant dans une matrice à résistances les deux sous porteuses.

Il est très intéressant de remarquer que le signal de chrominance ne comporte pas de composante continue (le signal de la (figure 58 c) est à cheval sur le niveau zéro).

L’absence de la composante continue traduit le fait que ce signal est indépendant de la luminance (principe même de la luminance constante).

Vous noterez, sur la (figure 57 b) , que les couleurs complémentaires donnent la même valeur d’amplitude du signal de chrominance et que leurs phases sont opposées (écart de 180°).

Ainsi, par exemple, si la phase du vecteur est de 173° pour la couleur jaune, la couleur bleue (complémentaire) correspond à une phase de + 180° par rapport à celle du jaune, donc 173° + 180° = 353° (figure 57 b) . Pour obtenir maintenant le signal vidéo complet, c'est-à-dire totalisant le signal de luminance et celui de chrominance, il suffit d’en faire la somme dans une matrice pour obtenir les valeurs indiquées à la (figure 58 e) .

Exemple pour la couleur bleue :

0,90 (chrominance) + 0,11 (luminance) = 1,01 (vidéo composite).

5) Compression du signal de chrominance

En observant la (figure 58 e) , vous remarquerez que le signal vidéo composite dépasse en valeurs positives, le maximum permis égal à 1 (blanc) et empiète largement en valeurs négatives, sur l’emplacement réservé aux signaux de synchronisation, malgré leur amplitude portée de 25 à 50%. Un tel signal produirait des distorsions inacceptables, puisque la modulation dépasse le 100% (blanc).

D’autre part, à la réception, on aurait des instabilités de l’image, car la modulation dépasserait le niveau maximum correspondant aux impulsions de synchronisation. Il fait donc réduire l’amplitude des composantes R’ – Y’ et B’ –Y’. Compte tenu du rapport signal/bruit qu’il faut conserver correct, il a été choisi de limiter à 33% la sur modulation au dessus du niveau du noir (figure 59) .

Pour arriver à ce résultat, on compresse le signal de chrominance de la (figure 58 c) et on obtient le signal de la (figure 59 a) . la (figure 59 b) représente le signal vidéo composite obtenu avec le signal chrominance compressé.

Vous noterez que maintenant le signal bleu ne peut plus perturber la synchronisation car jamais l’amplitude de ce signal ne dépasse le niveau de synchronisation.

Par contre, la sous porteuse dépasse encore dans le cas du cyan et du jaune saturés, le niveau de 100%. Il faudra donc s’attendre à des distorsions dans le cas de ces couleurs.

On aurait pu évidemment, réduire davantage les signaux R’ – Y’ et B’ – Y’ de façon à éviter ce dépassement.

Fort heureusement, on ne rencontre pratiquement jamais de couleurs saturées dans la nature, d’autre part, les distorsions apportées n’altèrent que très peu les teintes reproduites et l’œil moyen n’est pas capable d’apprécier ces distorsions.

En outre, il est préférable de ne pas réduire exagérément les signaux de façon à ne pas être gêné par le souffle des amplificateurs : le rapport signal/bruit doit être le plus élevé possible.

6) Phase et amplitude réelles de la sous- porteuse

Le fait de limiter à 33% la sur modulation confère au signal de chrominance les amplitudes suivantes : (figure 59)

Pour les plages bleues : 0,55 – 0,11 = 0,44

Pour les plages rouges : 0,93 – 0,30 = 0,63

Or, nous avions vu précédemment que l’amplitude de la sous -porteuse avant compression était égale pour les plages bleues à 0,896 et pour les plages rouges à 0,761 (figure 57 a) .

Rappelons comment nous avons obtenu ces deux valeurs :

0,761 = (1)

0,896 = (2)

Pour réduire l’amplitude de la sous -porteuse pour les plages rouges de 0,761 à 0,63 et pour les plages bleues de 0,896 à 0,44, il faut réduire l’amplitude des composants R’ – Y’ et B’ – Y’. Pour R’ – Y’, on réduit l’amplitude d’un facteur a et pour B’ – Y’ d’un facteur b.

Les équations (1) et (2) deviennent :

0,63 =

0,44 =

Elevons ces deux équations au carré :

(0,63) = 03969 = 0,49 a = 0,09 b (3)

(0,44) = 0,1936 = 0,0121 a + 0,7921 b (4)

Exprimons, à partir de l’équation (3) la valeur de b en fonction de a :

0,09 b = 0,3969 – 0,49 a d’où b =

Remplaçons dans l’équation (4), b par sa valeur :

0,1936 = 0,0121 a + 0,7921 .

0,1936 = 0,0121 a +

0,1936 = 0,0121 a + 3,4922 – 4,3122 a

Soit : 4,3001 a = 3,2986

a = = 0,7670 d’où : a = = 0,877

Calculons maintenant la valeur de b en se servant de l’équation (3) et en remplaçant a par sa valeur 0,7670 :

0,3969 = (0,49) (0,7670) + 0,09 b

0,3969 = 0,3751 + 0,09 b

0,09 b = 0,0218

b = = 0,24222 d’où : b = = 0,493

Ainsi, l’amplitude du signal rouge vaut maintenant 0 877 (R’ – Y’) et l’amplitude du signal bleu 0,493 (B’ – Y’).

Ainsi, l’amplitude et la phase de sous porteuse avec ces nouvelles valeurs sont pour le rouge :

Amplitude : 0,63

Phase : tg = = = - 4,1450

Ce qui correspond à un angle de 103,5°.

En faisant de même pour toutes les autres couleurs de la mire de barre, on obtient le tableau de la (figure 60 a) , ce qui permet ensuite de construire le cercle de la (figure 60 b) .

7) en positionnant la sous porteuse de telle sorte que celle-ci occupe la bande allouée, on obtient le spectre de la (figure 61) .

La sous porteuse étant positionnée à 4,1 MHz, on dispose de 0,9 MHz de bandes latérales.

Or, on constate que les axes R’ – Y’ et B’ – Y’ correspondent à des couleurs pour lesquelles le pouvoir de résolution de l’œil est relativement élevé.

Ces deux composantes nécessitent une bande passante d’au moins 1,3 MHz. Or, on constate sur la (figure 61) que c’est impossible à réaliser puisqu’on est limité à 0,9 MHz.

La solution consiste à réserver une bande assez large (1,3 à 1,8 MHz) à une composante I’. Cette composante se rapporte alors aux teintes pour lesquelles le pouvoir de résolution de l’œil est le plus élevé.

Comme on ne peut pas disposer d’une bande passante de 2,6 MHz (deux fois 1,3), on attribue à une seconde composante Q’ une bande beaucoup plus faible. Cette composante Q’ correspond aux teintes pour lesquelles le pouvoir de résolution de l’œil est faible.

Ceci conduit au spectre de la (figure 62) . On transmet ainsi la composante I’ à large bande, mais dont la bande latérale supérieure est rétrécie et la composante Q’ à bande étroite.

La sous porteuse est positionnée à 4,42 MHz soit 567 fois la demi fréquence ligne. Les composantes I’ et Q’ sont en quadrature tout comme les composantes R’ – Y’ et B’ – Y’ l’étaient.

Le décalage choisi entre les nouveaux systèmes I’ et Q’ et les anciens R’ – Y’ et B’ – Y’ est égal à 33° pour répondre au mieux aux exigences évoquées plus haut.

8) Formation des signaux I’ et Q’

De même que les signaux R’ – Y’ et B’ – Y’, les signaux I’ et Q’ sont, eux aussi, formés à l’aide des trois signaux primaires R’, G’ et B’ convenablement dosés.

Les signaux I’ et Q’ avant compression sont donnés par les deux relations suivantes :

I’ = cos 33° (R’ – Y’) – sin 33° (B’ – Y’)

Q’ = sin 33° (R’ – Y’) + cos 33° (B’ – Y’)

Voyons comment on arrive à ces deux relations, d’abord pour Q’.

Considérons la (figure 63) sur laquelle sont représentés les deux axes 0Q’ et 0I’. Le triangle 0Q’ B’ – Y’ est un triangle rectangle dont 0Q’ est l’hypoténuse.

D’après le théorème de Pythagore (0Q’) = (B’ – Y) + (R’ – Y’) en divisant les deux membres par 0Q’, on obtient :

0Q’ =

D’où : 0Q’ = +

0Q’ = (B’ – Y’) + (R’ – Y’) (1)

Or = cos 33° et = sin 33°

Remplaçons dans l’équation (1), ces deux termes par leur valeur, on obtient :

0Q’ = cos 33° (B’ – Y’) + sin 33° (R’ – Y’)

De même, pour I’ on a :

(0I’) = (R’ – Y’) + (B’ – Y’)

0I’ =

0I’ = +

0I’ = - (2)

Or : = cos 33° et - = sin 33°

Remplaçons dans l’équation (2), ces deux termes par leur valeur, nous obtenons :

0I’ = cos 33° (R’ – Y’) – sin 33° (B’ – Y’) , enfin : sin 33° = 0,5446 et cos 33° = 0,8387 donc :

I’ = 0,8387 (R’ – Y’) – 0,5446 (B’ – Y’)

Q’ = 0,5446 (R’ – Y’) + 0,8387 (B’ – Y’)

Nous savons, d’autre part, que ces signaux doivent être comprimés tout comme l’étaient les signaux précédents, afin d’éviter les distorsions et les perturbations dans la synchronisation.

Les signaux I’ et Q’ après compression sont donnés par :

I’ = 0,877 x - 0,493 x

Soit : I’ = 0,74 (R’ – Y’) – 0,27 (B’ – Y’) (3)

Et : Q’ = 0,877 x + 0,496 x

Soit : Q’ = 0,48 (R’ – Y’) + 0,41 (B’ – Y’) (4)

Au lieu d’exprimer les signaux I’ et Q’ en fonction de (R’ – Y’) et (B’ – Y’), on peut le faire en fonction des signaux primaires R’, G’ et B’ :

R’ – Y’ = R’ – (0,30 R’ + 0,59 G’ + 0,11 B’)

R’ – Y’ = 0,70 R’ – 0,59 G – 0,11 B’

B’ – Y’ = B’ – (0,30 R’ + 0,59 G’ + 0,11 B’)

B’ – Y’ = - 0,30 R’ – 0,59 G’ + 0,89 B’

Remplaçons R’ – Y’ et B’ – Y’ par leur valeur dans les équations (3) et (4) :

I’ = 0,74 (0,70 R’ – 0,59 G’ – 0,11 B’) – 0,27 (- 0,30 R’ – 0,59 G’ + 0,89 B’)

I’ = 0,60 R’ – 0,28 G’ – 0,32 B’

Q’ = 0,48 (0,70 R’ – 0,59 G’ – 0,11 B’) + 0,41 (- 0,30 R’ – 0,59 G’ + 0,89 B’)

Q’ = 0,21 R’ – 0,52 G’ + 0,31 B’

Exemple :

1) cas d’une plage blanche : (R’ = G’ = B’ = 1)

Y’ = 1 I’ = 0,60 – 0,28 – 0,32 = 0 Q’ = 0,21 – 0,52 + 0,31 = 0

2) Cas d’une plage grise : (R’ = G’ = B’ = 0 < k < 1

Y’ = k I’ = 0 Q’ = 0

De même pour une plage noire pour laquelle Y’ = 0, ainsi que I’ et Q’.

L’amplitude du signal couleur S’ (vecteur 0P de la (figure 63) ) sera donnée par :

S’ = 0P = , 0p étant l’hypoténuse du triangle rectangle.

Prenons l’exemple du jaune représenté par 0P (figure 63) :

0P = = 0,445 (système I’ et Q’)

Dans le système d’axes (R’ – Y’) (B’ – Y’) (figure 63) :

0P = = 0,45

Nous avons vu que les signaux I’ et Q’ pouvaient très bien remplacer (R’ – Y’) et (B’ – Y’) avec l’avantage supplémentaire d’une meilleure reproduction des teintes rouge orangé, vert, bleu vert et cœur de pigeon.

La (figure 64) représente le cercle des couleurs avec les axes (R’ – Y’) et (B’ – Y’), ainsi que les axes I’ et Q’.

C) Fréquences des différents signaux dans le système NTSC.

Le système étant compatible, l’information de luminance sera transmise avec toutes les caractéristiques d’une image en noir et blanc : en particulier, son spectre de fréquences sera le même que dans le standard noir et blanc, soit 4,5 MHz (standard américain).

Nous savons qu’il existe dans le spectre vidéo des emplacements libres où nous pourrons placer un spectre couleur, si la fréquence de la sous porteuse est judicieusement choisie.

Pour cela, la fréquence de la sous porteuse sera reliée à celle du balayage lignes, par la relation :

= (2 k + 1)

Nous choisirons la modulation d’amplitude pour la sous porteuse car elle permet de transmettre les deux informations de couleur.

Les informations de couleurs seront codées sous la forme de différences de couleurs (c'est-à-dire sous la forme de différences entre la luminance et les différentes chrominances) : (R’ – Y’) (B’ – Y’) ou encore I’ et Q’.

La fréquence de la sous porteuse sera la plus élevée possible, de façon à donner un brouillage aussi peu visible que possible.

Elle sera déterminée par la largeur maximum de la bande supérieure des canaux de chrominance que nous déciderons de transmettre.

Les couleurs voisines de l’axe rouge orangé et bleu vert (axe des pouvoirs de résolution élevés) seront transmises avec un spectre de 1,3 MHz.

Les couleurs voisines de l’axe des faibles pouvoirs de résolution (violet pourpre et jaune vert) seront transmises avec un spectre très réduit de l’ordre de 0,5 MHz.

Comme nous désirons réduire au maximum la visibilité de la sous porteuse, cette dernière sera supprimée et seules les bandes latérales seront transmises.

La sous porteuse étant supprimée, il faudra indiquer quelque part dans le signal transmis, la phase de référence des couleurs : ce qui sera le rôle des salves de couleurs (Color Bursts) qui seront transmises sous forme de huit alternances d’une sinusoïde à la fréquence de la sous porteuse immédiatement après les impulsions de synchronisation horizontale.

Nous savons qu’une modulation d’amplitude de deux sous porteuses de même fréquence mais en quadrature l’une par rapport à l’autre est équivalente à une modulation simultanée de phase et d’amplitude d’une sous porteuse unique.

Le signal I’ modulera en amplitude une sous porteuse .

Le signal Q’ modulera en amplitude une sous porteuse déphasée de 90° en arrière de la sous porteuse .

Les signaux R, G et B issus des caméras seront corrigés en gamma à l’émission.

1) Choix de la fréquence de la sous porteuse

Elle doit être aussi élevée que possible (pointillés fins).

Elle doit pouvoir être modulée, la limite supérieure du spectre vidéo est de 4,5 MHz et en prenant une marge de sécurité pour la bande latérale supérieure du canal Q’ (soit 0,9 MHz environ), la fréquence sera de l’ordre de :

4,5 – 0,9 = 3,6 MHz environ

Elle doit être multiple impair de la demi fréquence lignes :

= (2 k + 1) (1)

Il faut aussi que son battement avec la porteuse son , soit un multiple impair de la fréquence lignes :

- ( + ) = (2 k’ + 1) (2)

(k et k’ étant des nombres entiers quelconques).

Des relations (1) et (2), nous tirons :

Relation (1) + relation (2) :

+ - - = (2 k + 1) + (2 k’ + 1)

- = + + +

- = + +

- = (k + k’ + 1) = (3)

Avec m = k + k’ + 1 , nombre entier quelconque, or, ( - ) = 4,5 Mhz dans le standard noir et blanc.

D’autre part, la fréquence de balayage lignes en noir et blanc est :

= 525 lignes x = 15 750 Hz , 60 Hz est la fréquence du réseau USA, 525 lignes est le nombre de lignes choisi.

Il faut essayer de trouver une fréquence de balayage lignes pour la couleur la plus voisine possible de .

Les fréquences de balayage, tant lignes qu’images, sont obtenues par division de fréquence à partir d’un maître oscillateur.

Les fréquences les plus voisines de sont d’après la relation (3), pour m = 285 et m = 286.

= = = 15 789,47 Hz ou bien :

= = 15 734,26 MHz

Or, il s’avère plus facile de diviser 4,5 MHz par 286 que par 285. C’est donc la fréquence = 15 734,26 Hz qui a été choisie comme fréquence de balayage pour la couleur.

Quant à la fréquence de balayage vertical (images) ( = 60 Hz pour le noir et blanc), elle sera pour la couleur :

= = = 59,94 Hz = 59,94 Hz

La fréquence de la sous porteuse sera alors déterminée en multipliant par un nombre impair la demi fréquence lignes , le nombre obtenu devant être voisin de 3,6 MHz.

Le nombre le plus facile à obtenir est 455. La fréquence de la sous porteuse sera par conséquent :

= 455 x = 3,579545 MHz

2) Obtention des différentes fréquences

Un maître oscillateur général piloté par quartz délivre la fréquence de 3,579545 MHz (figure 65) .

La fréquence du maître oscillateur d’analyse est tirée à partir de celle du maître oscillateur général en divisant par 455, puis en multipliant par 4 sa fréquence.

On obtient : = = 31 468,52 Hz

Pour obtenir maintenant la fréquence de balayage lignes (pour la couleur), il suffit tout simplement de diviser par deux la fréquence  :

= = 15 734,26 Hz

Et pour obtenir la fréquence de balayage vertical (pour la couleur), il suffira de diviser par 525 la fréquence relation (4) :

= = 59,94 Hz

Comme d’autre part, la différence des fréquences entre la porteuse son ( ) et la porteuse image () doit être rigoureusement égale à 286 fois la fréquence de balayage lignes, on asservira l’oscillateur son par un comparateur de fréquences qui comparera les fréquences :

et

La (figure 65) donne le bloc diagramme des divisions successives de fréquences effectuées dans le système NTSC américain.

Les différences entre les fréquences et d’une part, et d’autre part, sont minimes et permettent aux différents oscillateurs du récepteur, de se synchroniser facilement, indifféremment sur une émission noir et blanc ou sur une émission couleurs.

Dans la (figure 66) est dressé un tableau comparatif noir et blanc et couleur, valable pour le système NTSC américain.

3) Système NTSC européen

Le système américain a été adapté pour les normes européennes (625 lignes et 50 Hz), dans le cas où ce système pourrait être normalisé sur le vieux continent.

Nous ne considérons ici que le cas pouvant intéresser la France où la séparation fréquence image- son est égale à 6,5 MHz (norme CCIR dite L).

La fréquence de balayages lignes (en couleurs) est par un hasard heureux la même que (en noir et blanc).

On a donc : = = 15 625 Hz

On a décidé de situer la fréquence de la sous porteuse vers 4,43 MHz. Le nombre impair le plus simple et le plus facile à obtenir qui permet de déterminer est 567. La fréquence de la sous porteuse est donc :

= x 567 = 4,429687 MHz

La fréquence de balayage vertical est la même couleur qu’en noir et blanc :

= = 50 Hz

Etant donné la position de la sous porteuse dans le spectre vidéo, il serait possible d’émettre les signaux de chrominance I’ et Q’ avec des bandes égales non atténuées, de 1,57 MHz chacune.

La bande latérale principale de luminance est en effet, égale à 6 MHz dans la norme CCIR L , d’où :

6 MHz – 4,43 MHz = 1,57 MHz

D’après ce que nous savons sur l’influence de la largeur de bande des signaux de chrominance sur la qualité finale de l’image, nous devrons nous attendre à une excellente reproduction des couleurs dans des conditions normales de propagation (figure 67) .

4) Le signal complet

Dans un cas comme dans l’autre, l’équation du signal en couleur complet sera :

= Y’ + I’ cos ( t + 33°) + Q’ sin ( t + 33°) , avec = la tension vidéo totale appliquée au modulateur de l’émetteur.

Dans le cas où l’on désirerait transmettre les signaux (R’ – Y’) et (B’ – Y’) à la place des signaux I’ et Q’, l’équation s’écrirait :

= Y’ + 0,877 (R’ – Y’) cos t + 0,493 (B’ – Y’) sin t

La (figure 68) montre comment le signal vidéo luminance et la sous porteuse de chrominance s’ajoutent pour constituer le signal global de modulation de l’émetteur. Les variations des tensions sont représentées en fonction du temps.

Le signal NTSC est très sensible aux distorsions de phase. Or, la phase d’un signal, surtout situé prés de la limite supérieure de la bande passante, est susceptible d’être perturbée par un grand nombre de causes. On peut classer ces causes en deux catégories :

Causes ne dépendant pas du signal : non linéarité de phase dans les circuits, variations du temps de propagation, réflexions parasites, dérive de l’oscillateur de référence dans le récepteur, etc. … La majorité de ces perturbations peuvent être maintenues à un niveau acceptable moyennant de grandes précautions dans les circuits de transmission.

Causes dépendant du niveau du signal : tous les amplificateurs ont une bande passante, donc une rotation de phase qui varie légèrement en fonction du niveau du signal qui leur est appliqué. Or, dans le système NTSC, le signal de référence de phase (Color Bursts) est transmis entre les lignes, c'est-à-dire toujours au niveau de modulation correspondant au noir.

Le signal de couleur, par contre, est superposé à un signal de luminance de niveau essentiellement variable. Il s’en suit un déphasage qu’il est pratiquement impossible de corriger, surtout dans les récepteurs.

Il suffit de se rappeler de ce défaut principal du système NTSC pour comprendre pourquoi ont été recherchés d’autres systèmes insensibles aux distorsions de phase.